题目内容
11. 如图,矩形纸片ABCD中,现将A、C重合,使纸片折叠压平,设折痕为EF,
如图,矩形纸片ABCD中,现将A、C重合,使纸片折叠压平,设折痕为EF,(1)连接CF,四边形AECF是什么特殊的四边形?为什么?
(2)若AB=4cm,AD=8cm,你能求出线段BE及折痕EF的长吗?
分析 (1)直接利用翻折变换的性质结合平行四边形的判定与性质以及结合菱形的判定方法得出答案;
(2)利用(1)中所求,结合勾股定理得出EF,BE的长.
解答 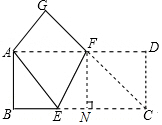 解:(1)四边形AECF是菱形,
解:(1)四边形AECF是菱形,
理由:连接CF,
∵矩形纸片ABCD中,现将A、C重合,
∴AE=EC,∠AEF=∠CEF,∠AFE=∠FEC,
∴∠AEF=∠AFE,
∴AF=AE,
可得:AF$\stackrel{∥}{=}$EC,
∴四边形AECF是平行四边形,
又∵AE=EC,
∴平行四边形AECF是菱形;
(2)设BE=x,则AE=8-x,
故在Rt△ABE中,
AB2+BE2=AE2,
即42+x2=(8-x)2,
解得:x=3,
即BE=3cm,
过点F作FN⊥BC于点N,
则FN=AB=4cm,
∵AF=AE=5cm,
∴EN=BN-BE=5cm-3cm=2cm,
∴在Rt△FEN中,EF=$\sqrt{E{N}^{2}+F{N}^{2}}$=2$\sqrt{5}$cm.
点评 此题主要考查了翻折变换的性质以及勾股定理、菱形的判定与性质等知识,正确掌握翻折变换的性质是解题关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
2.关于直线l:y=kx+k(k≠0),下列说法不正确的是( )
| A. | 点(0,k)在直线l上 | B. | 直线l经过定点(-1,0) | ||
| C. | 直线l经过第一、二、三象限 | D. | 当k>0时,y随x的增大而增大 |
6.把根式-a$\sqrt{-\frac{1}{a}}$化成最简二次根式为( )
| A. | $\sqrt{-a}$ | B. | $a\sqrt{-a}$ | C. | $-\sqrt{-a}$ | D. | -$a\sqrt{-a}$ |
 如图,立方体棱长为2cm,将线段AC平移到A1C1的位置上,平移的距离是2cm.
如图,立方体棱长为2cm,将线段AC平移到A1C1的位置上,平移的距离是2cm.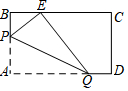 如图,矩形纸片ABCD,AB=3,AD=5,折叠纸片,使点A落在BC边上的E处,折痕为PQ,当点E在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点E在BC边上可移动的最大距离为2.
如图,矩形纸片ABCD,AB=3,AD=5,折叠纸片,使点A落在BC边上的E处,折痕为PQ,当点E在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点E在BC边上可移动的最大距离为2. 如图,已知点O为∠CAB与∠ACD的平分线的交点,OE⊥AC于E,若OE=2,则点O到AB的距离与点O到CD的距离之和是4.
如图,已知点O为∠CAB与∠ACD的平分线的交点,OE⊥AC于E,若OE=2,则点O到AB的距离与点O到CD的距离之和是4.