题目内容
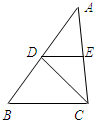 如图,已知CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
如图,已知CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.根据解题的要求,填写适当的内容或理由.
解:∵DE∥BC (已知)
∴∠ACB=∠AED=80° (
两直线平行,同位角相等
两直线平行,同位角相等
)∵CD平分∠ACB (已知)
∴∠DCB=∠DCA=40° (
角平分线的定义
角平分线的定义
)∵DE∥BC (已知)
∴∠EDC=∠DCB=40°(
两直线平行,内错角相等
两直线平行,内错角相等
)分析:根据平行线的性质,两直线平行,同位角相等,可得出结论,再由角平分线的定义,可得出∠DCB=∠DCA,最后根据两直线平行,内错角相等得∠EDC=∠DCB即可.
解答:解:∵DE∥BC (已知)
∴∠ACB=∠AED=80° (两直线平行,同位角相等 )
∵CD平分∠ACB (已知)
∴∠DCB=∠DCA=40° ( 角平分线的定义)
∵DE∥BC (已知)
∴∠EDC=∠DCB=40°(两直线平行,内错角相等 );
故答案为:两直线平行,同位错角相等;角平分线的定义;两直线平行,内错角相等.
∴∠ACB=∠AED=80° (两直线平行,同位角相等 )
∵CD平分∠ACB (已知)
∴∠DCB=∠DCA=40° ( 角平分线的定义)
∵DE∥BC (已知)
∴∠EDC=∠DCB=40°(两直线平行,内错角相等 );
故答案为:两直线平行,同位错角相等;角平分线的定义;两直线平行,内错角相等.
点评:本题考查了平行线的性质、角平分线的定义以及三角形的内角和定理,是基础知识要熟练掌握.

练习册系列答案
相关题目
 12、如图,已知CD平分∠ACB,DE∥BC,∠AED=80°,则∠EDC=
12、如图,已知CD平分∠ACB,DE∥BC,∠AED=80°,则∠EDC=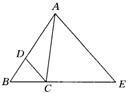 104、如图,已知CD平分∠ACB,AE∥DC,交BC延长线于点E,试说明△ACE是什么样的三角形.
104、如图,已知CD平分∠ACB,AE∥DC,交BC延长线于点E,试说明△ACE是什么样的三角形.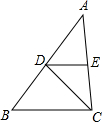 如图,已知CD平分∠ACB,DE∥BC,说明△EDC是等腰三角形的理由.
如图,已知CD平分∠ACB,DE∥BC,说明△EDC是等腰三角形的理由. 如图,已知CD平分∠ACB,交AB于D,AE∥CD,交BC的延长线于点E,且∠E=60°.你认为△ACE是什么三角形?请说明理由.
如图,已知CD平分∠ACB,交AB于D,AE∥CD,交BC的延长线于点E,且∠E=60°.你认为△ACE是什么三角形?请说明理由.