题目内容
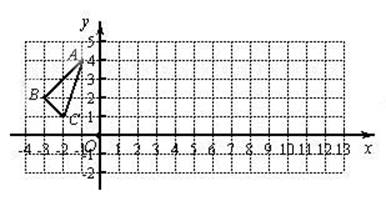
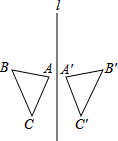如图，△ABC关于直线l做了轴反射后得到的像为△A′B′C′，且∠A=78°，∠C′=48°，∠B′=54°，∠C=48°，则∠B的度数为
- A.48°
- B.54°
- C.74°
- D.78°
B
分析：先根据轴对称的性质得出△ABC≌△A′B′C′，再根据全等三角形的性质即可得出结论．
解答：∵△ABC与△A′B′C′关于直线l对称，
∴△ABC≌△A′B′C′，
∴∠B=∠B′=54°．
故选B．
点评：本题考查的是轴对称的性质，熟知关于轴对称的两个图形全等是解答此题的关键．
分析：先根据轴对称的性质得出△ABC≌△A′B′C′，再根据全等三角形的性质即可得出结论．
解答：∵△ABC与△A′B′C′关于直线l对称，
∴△ABC≌△A′B′C′，
∴∠B=∠B′=54°．
故选B．
点评：本题考查的是轴对称的性质，熟知关于轴对称的两个图形全等是解答此题的关键．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
相关题目
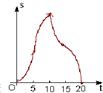
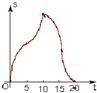
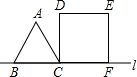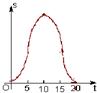
如图，（单位：cm）边长为10cm的等边△ABC以1cm/s的速度沿直线L向边长为10cm的正方形CDEF的方向移动，直到点B与点F重合，△ABC与正方形CDEF重叠部分的面积S关于平移动时间t的函数图象可能是（ ）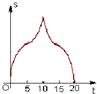
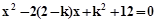有实数根α、β.求实数k的取值范围；设
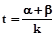，求t的最小值.