题目内容
在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，设BC=a，AC=b，若AB=16，且CD=6，那么a-b= ．
考点：相似三角形的判定与性质
专题：
分析：首先由勾股定理得到a和b的数量关系，再根据三角形的面积为定值又可以得到a和b的另外一对数量关系，进而可求出a-b的值．
解答：解：∵在Rt△ABC中，∠ACB=90°，
∴BC2+AC2=AB2，
∴AB2=a2+b2=256，
∵CD⊥AB
∴AB×CD=AC×BC=96，
∴16×6=ab=96，
∴（a-b）2=a2-2ab+b2=256-2×96=64，
∵a-b=8或-8．
∴BC2+AC2=AB2，
∴AB2=a2+b2=256，
∵CD⊥AB
∴AB×CD=AC×BC=96，
∴16×6=ab=96，
∴（a-b）2=a2-2ab+b2=256-2×96=64，
∵a-b=8或-8．
点评：本题考查了勾股定理的运用以及三角形面积公式的运用，解题的关键是利用整体思路求出a-b的值，显然此题也可以通过相似三角形的有关知识解决．
练习册系列答案
相关题目
如图，下列语句错误的是（ ）| A、点0在直线AB上 |
| B、点0在射线BA上 |
| C、点B是线段AB的一个端点 |
| D、射线AB和射线BA是同一条射线 |
如图，直线AD∥BE∥CF，
如图，函数y=2x和y=ax+4的图象相交于点A（1，2），则不等式2x≥ax+4的解集为（ ）| A、x＜1 | B、x＞1 |
| C、x≤1 | D、x≥1 |
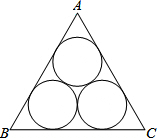如图，三个半径为| 3 |
A、12+6
| ||
B、12+12
| ||
C、18+12
| ||
D、18+6
|
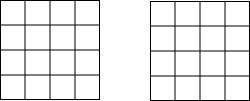如图是两个4×4的正方形网格，在每个网格中，把其中的5个小正方形涂上阴影，使整个图案为轴对称图形．