Question

【题目】如图，Q是上一定点，P是弦AB上一动点，C为AP中点，连接CQ，过点P作交于点D，连接AD，CD．

已知，设A，P两点间的距离为，C，D两点间的距离为．

（当点P与点A重合时，令y的值为1.30）

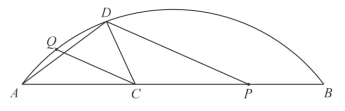
小荣根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探宄．

下面是小荣的探究过程，请补充完整：

（1）按照下表中自变量x的值进行取点、画图、测量，得到了y与x的几组对应值：

（2）建立平面直角坐标系，描出以补全后的表中各组对应值为坐标的点，画出该函数的图象；

（3）结合函数图象，解决问题：当时，AP的长度约为__________cm．

Answer 1

【答案】（1）1.85；（2）见解析；（3）3.31

【解析】

（1）根据题意，通过取点、画图、测量可得；

（2）描点，用光滑的曲线连接；

（3）当，可知,结合,即 ，可知两个函数图像交点横坐标即为所求 .

解：(1) 根据题意，通过取点、画图、测量可得：当时，

(2) 描点，用光滑的曲线连接，如下图所示：

（3） ，

, ,

即 ，画出函数图像

可知两个函数图像交点横坐标约为 ，即 .

故答案为：