Question

【题目】在中，、相交于点分别是中点，连接．

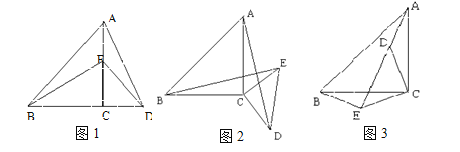
（1）如图1，求证：四边形是平行四边形；

（2）如图2，若，求证：四边形是矩形．

Answer 1

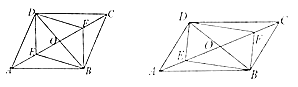
【答案】（1）见详解；（2）见详解．

【解析】

（1）通过得OA＝OC，OB＝OD，结合分别是中点得OE＝OF，再利用对角线互相平分的四边形是平行四边形即可得证；

（2）通过结合得，再利用对角线相等的平行四边形是矩形即可得证．

证明：（1）∵在中，

∴OA＝OC，OB＝OD，

∵分别是中点，

∴OE＝OA，OF＝OC，

∴OE＝OF，

∵OE＝OF，OB＝OD，

∴四边形是平行四边形；

（2）∵OE＝OA，OF＝OC，

∴OE＋OF＝OA＋OC＝(OA＋OC)＝AC，

即：EF＝AC，

∵，

∴BD＝AC，

∴BD＝EF，

∵四边形是平行四边形，BD＝EF，

∴四边形是矩形．