题目内容
【题目】如图，点C是半圆O上的一点，AB是⊙O的直径，D是
的中点，作DE⊥AB于点E，连接AC交DE于点F，求证：AF=DF.
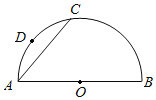
下面是小明的做法，请帮他补充完整（包括补全图形）
解：补全半圆O为完整的⊙O，连接AD，延长DE交⊙O于点H（补全图形）
∵D是的中点，
∴
.
∵DE⊥AB，AB是⊙O的直径，
∴
（ ）（填推理依据）
∴
∴∠ADF=∠FAD（ ）（填推理依据）
∴AF=DF（ ）（填推理依据）
【答案】垂径定理，等弧所对的圆周角相等，等角对等边．
【解析】
利用圆周角定理以及垂径定理证明∠ADF=∠FAD即可解决问题．
补全半圆O为完整的⊙O，连结AD，延长DE交⊙O于点H（补全图形）．
∵D是
的中点，
∴
.
∵DE⊥AB，AB是⊙O的直径，
∴
（垂径定理）
∴
∴∠ADF=∠FAD（等弧所对的圆周角相等）
∴AF=DF（等角对等边）
故答案为：垂径定理，等弧所对的圆周角相等，等角对等边．
练习册系列答案
相关题目
