题目内容
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .点
.点![]() 在
在![]() 轴的负半轴上,且
轴的负半轴上,且![]() 的面积为8,直线
的面积为8,直线![]() 和直线
和直线![]() 相交于点
相交于点![]() .
.
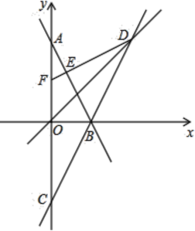
(1)求直线![]() 的解析式;
的解析式;
(2)在线段![]() 上找一点
上找一点![]() ,使得
,使得![]() ,线段
,线段![]() 与
与![]() 相交于点
相交于点![]() .
.
①求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上,且
轴上,且![]() ,直接写出
,直接写出![]() 的长为 .
的长为 .
【答案】(1)直线![]() 的解析式为
的解析式为![]() ;(2)①
;(2)①![]() ,
,![]() ,②满足条件的
,②满足条件的![]() 的值为8或
的值为8或![]() .
.
【解析】
(1)求出B,C两点坐标,利用待定系数法即可解决问题.
(2)①连接AD,利用全等三角形的性质,求出直线DF的解析式,构建方程组确定交点E坐标即可.
②如图1中,将线段FD绕点F顺时针旋转90°得到FG,作DE⊥y轴于E,GH⊥y轴于F.根据全等三角形,分两种情形分别求解即可.
(1)![]() 直线
直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
![]() ,
,![]() ,
,
![]() 点
点![]() 在
在![]() 轴的负半轴上,且
轴的负半轴上,且![]() 的面积为8,
的面积为8,
![]()
![]() ,
,
![]() ,则
,则![]() ,
,
设直线![]() 的解析式为
的解析式为![]() 即
即![]() ,
,
解得![]() ,
,
故直线![]() 的解析式为
的解析式为![]() .
.
(2)①连接![]() .
.

![]() 点
点![]() 是直线
是直线![]() 和直线
和直线![]() 的交点,故联立
的交点,故联立![]() ,
,
解得![]() ,即
,即![]() .
.
![]() ,故
,故![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
即![]() ,可求直线
,可求直线![]() 的解析式为
的解析式为![]() ,
,
![]() 点
点![]() 是直线
是直线![]() 和直线
和直线![]() 的交点,
的交点,
故联立 ,解得
,解得 ,
,
即![]() ,
,![]() .
.
②如图1中,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,作
,作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() .
.

则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
设直线![]() 交
交![]() 轴于
轴于![]() ,则
,则![]() ,
,
![]() ,
,
![]() .
.
作![]() ,则
,则![]() ,
,
可得直线![]() 的解析式为
的解析式为![]() ,
,
![]() ,
,
![]() ,
,
综上所述,满足条件的![]() 的值为8或
的值为8或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目