题目内容
在△ABC中,∠A为锐角,CD⊥AB于D,且CD2=AD•BD,那么△ABC是________三角形(按角分类).
直角
分析:由CD⊥AB,得到∠CDA=∠CDB=90°,而CD2=BD•AD,即CD:BD=AD:CD,根据三角形相似的判定定理得到△ADC∽△CDB,则∠A=∠DCB,而∠A+∠ACD=90°,即可得到∠ACD+∠DCB=90°.
解答: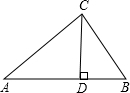 解:如图,
解:如图,
∵CD⊥AB,
∴∠CDA=∠CDB=90°,
∵CD2=BD•AD,即CD:BD=AD:CD,
∴△ADC∽△CDB,
∴∠A=∠DCB,
而∠A+∠ACD=90°,
∴∠ACD+∠DCB=90°,
∴△ABC是直角三角形,
故答案为:直角.
点评:本题主要考查了三角形相似的判定与性质:如果两个三角形的两条对应边的比相等,并且它们的夹角也相等,那么这两个三角形相似;相似三角形的对应角相等,难度适中.
分析:由CD⊥AB,得到∠CDA=∠CDB=90°,而CD2=BD•AD,即CD:BD=AD:CD,根据三角形相似的判定定理得到△ADC∽△CDB,则∠A=∠DCB,而∠A+∠ACD=90°,即可得到∠ACD+∠DCB=90°.
解答:
 解:如图,
解:如图,∵CD⊥AB,
∴∠CDA=∠CDB=90°,
∵CD2=BD•AD,即CD:BD=AD:CD,
∴△ADC∽△CDB,
∴∠A=∠DCB,
而∠A+∠ACD=90°,
∴∠ACD+∠DCB=90°,
∴△ABC是直角三角形,
故答案为:直角.
点评:本题主要考查了三角形相似的判定与性质:如果两个三角形的两条对应边的比相等,并且它们的夹角也相等,那么这两个三角形相似;相似三角形的对应角相等,难度适中.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 已知:如图,在△ABC中,AD为BC边上的高,∠B=45°,∠C=30°,AD=2.求△ABC的面积.
已知:如图,在△ABC中,AD为BC边上的高,∠B=45°,∠C=30°,AD=2.求△ABC的面积.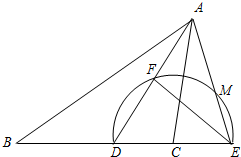 AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.
AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.
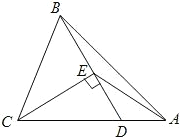
 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是76cm2,AB=20cm,AC=18cm,求DE的长.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是76cm2,AB=20cm,AC=18cm,求DE的长.