题目内容
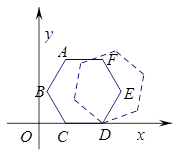
已知在平面直角坐标系中依次放置了n个如图所示的正方形,点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形 的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3∥…∥BnCn,则点A2013到x轴的距离是 ( )
的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3∥…∥BnCn,则点A2013到x轴的距离是 ( )

 的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3∥…∥BnCn,则点A2013到x轴的距离是 ( )
的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3∥…∥BnCn,则点A2013到x轴的距离是 ( )
A.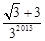 | B. | C. | D. |
B
试题分析:利用正方形的性质以及平行线的性质分别得出D1E1=B2E2=
 ,B2C2=
,B2C2= ,进而得出B3C3=
,进而得出B3C3= ,求出WQ=
,求出WQ= ×
× =
= ,FW=WA3•cos30°=
,FW=WA3•cos30°= ×
× =
= ,即可得出规律,求得结果.
,即可得出规律,求得结果.过小正方形的一个顶点W作FQ⊥x轴于点Q,过点A3F⊥FQ于点F,

∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,
∴∠B3C3 E4=60°,∠D1C1E1=30°,∠E2B2C2=30°,
∴D1E1=
 D1C1=
D1C1= ,
,∴D1E1=B2E2=
 ,
,
解得B2C2=

∴B3E4=


解得B3C3=

则WC3=

根据题意得出:∠WC3 Q=30°,∠C3 WQ=60°,∠A3 WF=30°,
∴WQ=
 ×
× =
=
FW=WA3•cos30°=
 ×
× =
=
则点A3到x轴的距离是:FW+WQ=
 +
+
所以点A2013到x轴的距离是

故选B.
点评:解答此类问题的关键是仔细分析所给图形的特征得到规律,再把这个规律应用于解题.

练习册系列答案
相关题目
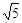
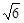

 、
、 分别是
分别是 与
与 的图象上的点,且
的图象上的点,且



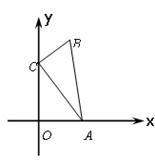
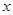 轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(45,2)的是点 .
轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(45,2)的是点 .