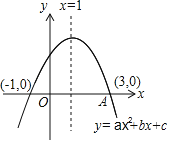Question

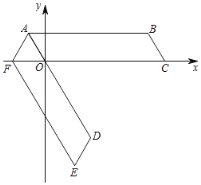
【题目】如图，在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）的顶点为A（﹣2，0），且经过点B（﹣5，9），与y轴交于点C，连接AB，AC，BC．

（1）求该抛物线对应的函数表达式；

（2）点P为该抛物线上点A与点B之间的一动点．

①若S△PAB＝S△ABC，求点P的坐标．

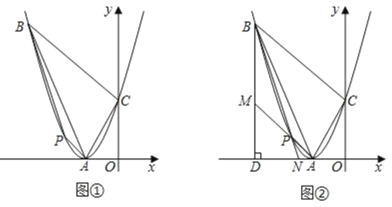
②如图②，过点B作x轴的垂线，垂足为D，连接AP并延长，交BD于点M．连接BP并延长，交AD于点N．试说明DN（DM+DB）为定值．

Answer 1

【答案】（1）y＝x2+4x+4；（2）①P（﹣3，1）或（﹣4，4）；②见解析，DN（DM+DB）为定值27．

【解析】

（1）利用顶点式设出抛物线解析式，再将点B坐标代入求解，即可得出结论；

（2）先求出直线BC解析式，进而求出三角形ABC的面积，得出三角形ABP的面积为3，设出点P坐标，表示出点G坐标，利用三角形ABP的面积为3建立方程求解即可得出结论；

②先设出直线BN的解析式y＝k（x＋5）＋9①，得出DN，再设出直线AM的解析式为y＝k'（x＋2）②，进而得出DM，再联立①②求出点P坐标，再将点P坐标代入抛物线解析式中，得出k＝k'3，即可得出结论．

解：（1）∵抛物线y＝ax2+bx+c（a≠0）的顶点为A（﹣2，0），

∴设抛物线的解析式为y＝a（x+2）2，

将点B（﹣5，9）代入y＝a（x+2）2中，得，9＝a（﹣5+2）2，

∴a＝1，

∴抛物线的解析式为y＝（x+2）2＝x2+4x+4；

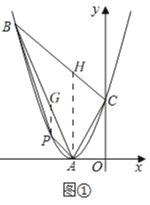
（2）①如图①，由（1）知，抛物线的解析式为y＝x2+4x+4，

∴C（0，4），

∵B（﹣5，9），

∴直线BC的解析式为y＝﹣x+4，

过点A作AH∥y轴，交直线BC于H，

过P作PG∥y轴，交直线BA于HG，

∵A（﹣2，0），

∴H（﹣2，6），

∴S△ABC＝AH×（xC﹣xB）＝×6×5＝15，

∵S△PAB＝S△ABC，

∴S△PAB＝×15＝3，

∵A（﹣2，0），B（﹣5，9），

∴直线AB的解析式为y＝﹣3x﹣6

设点P（p，p2+4p+4），

∴G（p，﹣3p﹣6），

∴S△PAB＝ [﹣3p﹣6﹣（p2+4p+4）]×（﹣2+5）＝3，

∴p＝﹣3或p＝﹣4，

∴P（﹣3，1）或（﹣4，4）；

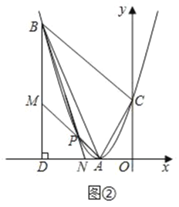
②如图②，

∵BD⊥x轴，且B（﹣5，9），

∴D（﹣5，0），

设直线BN的解析式为y＝k（x+5）+9①，

令y＝0，则k（x+5）+9＝0，

∴x＝﹣＝﹣5﹣，

∴N（﹣5﹣，0），

∴DN＝﹣5﹣+5＝﹣，

∵点A（﹣2，0），

∴设直线AM的解析式为y＝k'（x+2）②，

当x＝5时，y＝﹣3k'，

∴M（﹣5，﹣3k'），

∴DM＝﹣3k'，

联立①②得，

解得，，

∴P（﹣2﹣2×，﹣3k'×），

∵点P在抛物线y＝（x+2）2上，

∴（﹣2﹣3×+2）2＝﹣3k'×，

∴，

∴k＝k'﹣3，

∴DN（DM+DB）＝﹣（﹣3k'+9）＝27×（k'﹣3）＝27××k＝27；

即：DN（DM+DB）为定值27．