题目内容
分别以Rt△ABC的三边为直径作半圆M、N、P（如图所示），已知半圆M、N的面积分别为2πcm2、4πcm2，则半圆P的面积为分析：由题意由a，b，c分别表示半圆M，N，P的直径，用a，b，c表示出三个半圆面积，其相比即得到半圆P的面积．结合直角三角形中三边关系解得．
解答：解：半圆M面积=
π(
)2=
πa2
半圆N面积=
π b2
半圆P面积=
πc2
则：
πa2+
π b2=
πc2=2π+4π=6π（cm2）．
故应填6πcm2．
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 8 |
半圆N面积=
| 1 |
| 8 |
半圆P面积=
| 1 |
| 8 |
则：
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
故应填6πcm2．
点评：本题考查了勾股定理，把直角三角形的三边同圆联系起来，考查了学生的灵活机动的能力．
练习册系列答案
金钥匙试卷系列答案
相关题目
19、如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．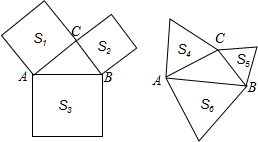
如图，若分别以Rt△ABC的三边为边长作正方形的面积分别是S1，S2，S3，其中∠BCA=90°，则可推得它们满足的关系式是S1+S2=S3．若分别以Rt△ABC的三边为边长作正三角形的面积分别是S4，S5，S6，那么S4，S5，S6满足的关系式是
如图，分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE，F为AB的中点，连接DF、EF、DE，EF与AC交于点O，DE与AB交于点G，连接OG，若∠BAC=30°，下列结论：①△DBF≌△EFA；②AD=AE；③EF⊥AC；④AD=4AG；⑤△AOG与△EOG的面积比为1：4．
如图，分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE，F为AB中点，连接DF、EF，DE、EF与AC交于点O，DE与AB交于点G，连接OG，若∠BAC=30°，下列结论：①△DBF≌△EFA；②AD=AE；③EF⊥AC；④AD=4AG；⑤△AOG与△EOG的面积比为1：4．其中正确的结论的序号是
如图，分别以Rt△ABC的三边为边向外作三个正方形，其面积分别用S1、S2、S3表示，请写出S1、S2、S3之间的关系，并说明理由．