题目内容
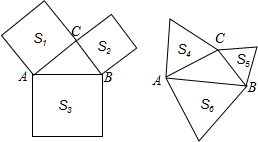如图，若分别以Rt△ABC的三边为边长作正方形的面积分别是S1，S2，S3，其中∠BCA=90°，则可推得它们满足的关系式是S1+S2=S3．若分别以Rt△ABC的三边为边长作正三角形的面积分别是S4，S5，S6，那么S4，S5，S6满足的关系式是分析：有S1+S2=S3得到Rt△ABC三边关系，有Rt△ABC三边得到的三个正三角形的面积，有边角关系面积公式从而得到．
解答：解：设BC=a，AC=b，AB=c．
则S1+S2=S3，
即b2+a2=c2①
右边角关系面积公式得s4=
b2sin60°，s5=
a2sin60°，s6=
c2sin60°．
∴b2=
，a2=
，c2=
．②
②代入①得：s4+s5=s6
则S1+S2=S3，
即b2+a2=c2①
右边角关系面积公式得s4=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴b2=
| 2s4 |
| sin60° |
| 2s5 |
| sin60° |
| 2s6 |
| sin60° |
②代入①得：s4+s5=s6
点评：本题考查了勾股定理的进一步运用，正确理解和灵活运用勾股定理．
练习册系列答案
快捷英语周周练系列答案
相关题目
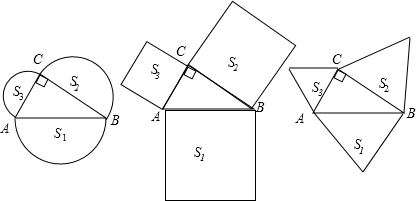
如图，若分别以Rt△ABC的三边为边长作正方形的面积分别是S1，S2，S3，其中∠BCA=90°，则可推得它们满足的关系式是S1+S2=S3．若分别以Rt△ABC的三边为边长作正三角形的面积分别是S4，S5，S6，那么S4，S5，S6满足的关系式是________．