Question

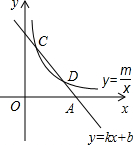如图，反比例函数y=

m

x

的图象在第一象限的一支上有一点C（1，3），经过点C的直线y=-kx+b（k＞0）于x轴交于点A（a，0）．
（1）求点A的横坐标a与k之间的函数关系式；
（2）当这条直线与反比例函数图象在第一象限的另一个交点D的横坐标为6时，求△COA的面积．

Answer 1

分析：（1））利用待定系数法把点C（1，3），A（a，0）代入y=-kx+b中即可得到a=1+

3

k

；
（2）利用待定系数法把点C（1，3）在反比例函数图象上，可求反比例函数的解析式；进而根据a与k之间的函数关系式可得D点坐标，再利用待定系数法求出一次函数解析式，进而求出直线与x轴交点坐标，即可求出△COA的面积．

解答：解：（1）∵点C（1，3），A（a，0）在y=-kx+b上，
∴

3=-k+b 0=-ak+b

，
∴a=1+

3

k

；

（2））∵点C（1，3）在反比例函数图象上，
∴k=1×3=3，
∴y=

3

x

，
∴D（6，

1

2

），
∵C、D在y=kx+b上，
∴

1 2 =-6k+b 3=-k+b

，
∴

k= 1 2 b= 7 2

，
∴a=7，
∴S_△COA=

1

2

×7×3=10.5．

点评：此题主要考查了反比例函数、一次函数的图象和性质．关键是熟练掌握待定系数法求函数关系式．