题目内容
 如图,AD,CE分别是△ABC的角平分线,它们的交点为F.若∠B=60°,∠ACB=72°,则∠BDA=
如图,AD,CE分别是△ABC的角平分线,它们的交点为F.若∠B=60°,∠ACB=72°,则∠BDA=24°
24°
;若∠B=60°,∠BAC=48°,则∠DFC=60°
60°
;若∠B=50°,则∠AFC=120°
120°
.分析:先根据三角形内角和定理求出∠BAC的度数,再由角平分线的定义即可得出∠BAD的度数;先根据角平分线的性质求出∠BAD的度数,根据三角形外角的性质求出∠ADC的度数,进而可得出∠DFC的度数;直接根据三角形外角的性质即可求出∠AFC的度数.
解答:解:∵AD,CE分别是△ABC的角平分线,∠B=60°,∠ACB=72°,
∴∠BAC=180°-60°-72°=48°,
∴∠BAD=
∠BAC=24°;
∵∠B=60°,∠BAC=48°,
∴∠ACB=180°-60°-48°=72°,
∵AD,CE分别是△ABC的角平分线,
∴∠BAD=
∠BAC=
×48°=24°,∠DCF=
∠ACB=
×72°=36°,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=60°+24°=84°,
∴∠DFC=180°-∠AC-∠DCE=180°-84°-36°=60°;
∴∠AFC=180°-∠DFC=180°-60°=120°.
故答案为:24°,60°,120°.
∴∠BAC=180°-60°-72°=48°,
∴∠BAD=
| 1 |
| 2 |
∵∠B=60°,∠BAC=48°,
∴∠ACB=180°-60°-48°=72°,
∵AD,CE分别是△ABC的角平分线,
∴∠BAD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=60°+24°=84°,
∴∠DFC=180°-∠AC-∠DCE=180°-84°-36°=60°;
∴∠AFC=180°-∠DFC=180°-60°=120°.
故答案为:24°,60°,120°.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
 如图,点D,E分别在AB,AC上,且AD=AE,∠BDC=∠CEB.
如图,点D,E分别在AB,AC上,且AD=AE,∠BDC=∠CEB. 21、如图,点D、E分别在AC、BC上,如果测得CD=20m,CE=40m,AD=100m,BE=20m,DE=45m,求A、B两地间的距离.
21、如图,点D、E分别在AC、BC上,如果测得CD=20m,CE=40m,AD=100m,BE=20m,DE=45m,求A、B两地间的距离. 4、如图,AD=DE=BE,那么图中有
4、如图,AD=DE=BE,那么图中有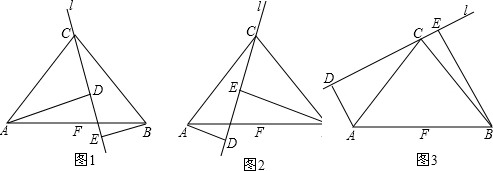
 画图题:如图在△ABC中,分别画出:
画图题:如图在△ABC中,分别画出: