题目内容
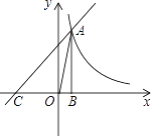
【题目】如图,在直角坐标系中,直线y=x+m与y=![]() 在第一象限交于点A,且与x轴交于点C,AB⊥x轴,垂足为B,且S△AOB=1.
在第一象限交于点A,且与x轴交于点C,AB⊥x轴,垂足为B,且S△AOB=1.
(1)求m的值;
(2)求△ABC的面积.
【答案】(1)m=2;(2)2+![]() .
.
【解析】分析:(1)、根据△AOB的面积得出m的值;(2)、根据m的值得出反比例函数和一次函数,然后求出点A和点C的坐标,从而得出三角形的面积.
详解:(1)、解:设A(x,y), ∵直线y=x+m与双曲线y= ![]() 在第一象限交于点A,S△AOB=1,
在第一象限交于点A,S△AOB=1,
∴ ![]() xy=1,即xy=m=2, ∴m=2
xy=1,即xy=m=2, ∴m=2
(2)、解:∵m=2, ∴直线方程为y=x+2, 令y=0,得x=﹣2, ∴C点坐标为(﹣2,0)
联立两函数的方程  , 解得A点坐标为(
, 解得A点坐标为(![]() ﹣1,
﹣1, ![]() +1),
+1),
∴BC=![]() +1, ∴S△ABC=
+1, ∴S△ABC= ![]() ×(
×(![]() +1)×(
+1)×(![]() +1)=2+
+1)=2+![]() .
.

练习册系列答案
相关题目