题目内容
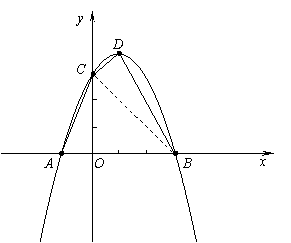
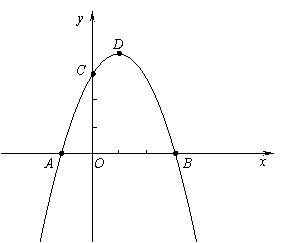
如图, 在平面直角坐标系中,二次函数
在平面直角坐标系中,二次函数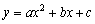 (
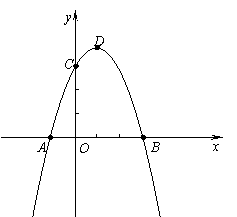
( )的图象经过点A(-1,0)、
)的图象经过点A(-1,0)、
点B(3,0)、点C(0,3).
(1)求此抛物线的解析式及顶点D的坐标;
(2)连结AC、CD、BD,试比较∠BCA与∠BDC的大小,并说明理由;
 (3)若在x轴上有一动点M,在抛物线
(3)若在x轴上有一动点M,在抛物线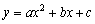 上有一动点N,则M、N、B、C四点是否能构成平行四边形,若存在,请求出所有适合的点M的坐标;若不存在,请说明理由.
上有一动点N,则M、N、B、C四点是否能构成平行四边形,若存在,请求出所有适合的点M的坐标;若不存在,请说明理由.
|
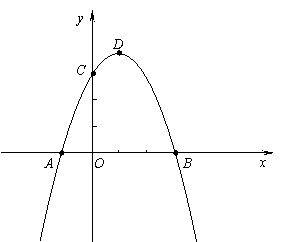 解:(1)∵点A、B、C在抛物线
解:(1)∵点A、B、C在抛物线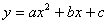 上,
上,
∴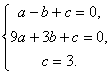 解得
解得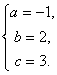
∴此抛物线为: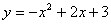 ………2分
………2分
由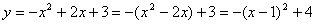
∴抛物线的顶点D的坐标为(1,4). ………4分
(2)连结BC,
由点C(0,3)、B(3,0)、D(1,4)
 可得CD=
可得CD=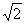 ,BD=
,BD=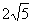 ,CB=
,CB=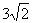
由点C(0,3)、A(-1,0),可得AC=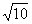
由
∴△CDB∽△OAC ∴∠BCA=∠BDC ………8分
(3)设点M的坐标为(t,0)
则由C(0,3)、B(3,0)、M(t,0)可以得到
若能构成平行四边形时点N的坐标有三种可能,
 分别是(3-t,3),(t-3,3),(t+3,-3)
分别是(3-t,3),(t-3,3),(t+3,-3)
∵点N在抛物线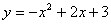 上
上
当把(3-t,3)代入时,
可得t=1或t=3(点M与点B重 合,舍去);
合,舍去);
当把(t-3,3)代入时,
可得t=5或t=3(点M与点B重合,舍去);
当把(t+3,-3)代入时,
可得t=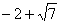 或t=
或t=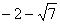 ,
,
综上可知,M的坐标为(1,0)、(5,0)、(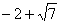 ,0)、(
,0)、(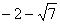 ,0).
,0).

练习册系列答案
相关题目


 .
. 且
且 ,
, ,则
,则 的值为 ………………………… ( )
的值为 ………………………… ( ) B.1 C.
B.1 C. D.
D.
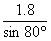 m D、
m D、 m
m