Question

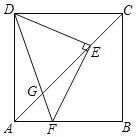
【题目】如图，正方形ABCD中，AB＝3，点E是对角线AC上的一点，连接DE，过点E作EF⊥DE，交AB于点F，连接DF交AC于点G，下列结论：

①DE＝EF；②∠ADF＝∠AEF；③DG2＝GEGC；④若AF＝1，则EG＝，其中结论正确的个数是（　　）

A. 1B. 2C. 3D. 4

Answer 1

【答案】D

【解析】

证明△DCE≌△BCE，得DE＝BE，证出EF＝BE，则结论①正确；易证∠EDF＝∠DFE＝45°，又∠DAC＝45°，∠AGD＝∠EGF，则∠ADF＝∠AEF，故②正确；证出△DGE∽△CGD，由比例线段可得出结论DG2＝GEGC，③正确；先求出CE长，将△DEC绕点A逆时针旋转90°得到△DMA，连接MG，易证△DMG≌△DEG，△AMG是直角三角形，得出EG2＝AG2+CE2，设EG＝x，则列出方程可求出EG＝，则④正确．

解：如图，连接BE，

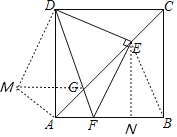
∵四边形ABCD为正方形，

∴CB＝CD，∠BCE＝∠DCE＝45°，

在△BEC和△DEC中，

，

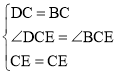∴△DCE≌△BCE（SAS），

∴DE＝BE，∠CDE＝∠CBE，

∴∠ADE＝∠ABE，

∵∠DAB＝90°，∠DEF＝90°，

∴∠ADE+∠AFE＝180°，

∵∠AFE+∠EFB＝180°，

∴∠ADE＝∠EFB，

∴∠ABE＝∠EFB，

∴EF＝BE，

∴DE＝EF，故①正确；

∵∠DEF＝90°，DE＝EF，

∴∠EDF＝∠DFE＝45°，

∵∠DAC＝45°，∠AGD＝∠EGF，

∴∠ADF＝∠AEF，故②正确；

∵∠GDE＝∠DCG＝45°，∠DGE＝∠CGD，

∴△DGE∽△CGD，

∴，

即DG2＝GECG，故③正确；

如图，过点E作EN⊥AB于点N，

∵AF＝1，AB＝3，

∴BF＝2，AC＝，

∵BE＝EF，

∴FN＝BN＝1，

∴AN＝2，

∴，

∴，

将△DEC绕点A逆时针旋转90°得到△DMA，连接MG，

易证△DMG≌△DEG（SAS），△AMG是直角三角形，

∴MG＝GE，

∴MG2＝EG2＝AM2+AG2＝CE2+AG2，

设EG＝x，则AG＝，

∴，

解得：x＝，即EG＝，故④正确．

故选：D．