题目内容
 直线y=-
直线y=-| 1 | 3 |
(1)写出点A、B、C、D的坐标;
(2)求经过A、C、D三点的抛物线表达式,并求抛物线顶点G的坐标;
(3)在直线BG上是否存在点Q,使得以点A、B、Q为顶点的三角形与△COD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
分析:(1)求出直线与x轴、y轴的交点坐标,得到△AOB,旋转后得到△COD,由图即可得到点A、B、C、D的坐标;
(2)设出二次函数的一般式,将A、C、D三点的坐标代入列出方程组即可求解;
(3)先假设存在,根据相似三角形的判定列出比例式,计算点Q的坐标,若能计算出来,则存在;否则不存在.
(2)设出二次函数的一般式,将A、C、D三点的坐标代入列出方程组即可求解;
(3)先假设存在,根据相似三角形的判定列出比例式,计算点Q的坐标,若能计算出来,则存在;否则不存在.
解答: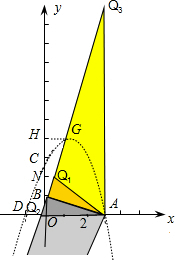 解:(1)A(3,0),B(0,1),C(0,3),D(-1,0);(4分)
解:(1)A(3,0),B(0,1),C(0,3),D(-1,0);(4分)
(2)∵抛物线y=ax2+bx+c经过C点,
∴c=3.(1分)
又∵抛物线经过A,D两点,
∴
,
解得
(2分)
∴y=-x2+2x+3(1分)
∴y=-x2+2x+3=-(x-1)2+4,
∴顶点G(1,4).(1分)
(3)解:过点G作GH⊥y轴垂足为点H,
∵AB=
,BG=
,
∵tan∠BAO=
,tan∠GBH=
,
∴∠BGH=∠BAO(1分)
∵∠BAO+∠ABO=90°,
∴∠BGH+∠ABO=90°,
∴∠GBA=90°,
∴∠ABQ=∠DOC=∠AOB(1分)
①当
=
时,△ODC∽△BQA,
即
=
,
∴BQ=
(1分)
过点Q作QN⊥y轴,垂足为点N,设Q(x,y),
∵
=
,
=
,|x|=
,x=±
∵tan∠GBH=
,
∴BN=1,
∴Q1(
,2),Q2(-
,0)(2分)
②同理可得:Q3(3,10),Q4(-3,-8).(2分)
 解:(1)A(3,0),B(0,1),C(0,3),D(-1,0);(4分)
解:(1)A(3,0),B(0,1),C(0,3),D(-1,0);(4分)(2)∵抛物线y=ax2+bx+c经过C点,
∴c=3.(1分)
又∵抛物线经过A,D两点,
∴
|
解得
|
∴y=-x2+2x+3(1分)
∴y=-x2+2x+3=-(x-1)2+4,
∴顶点G(1,4).(1分)
(3)解:过点G作GH⊥y轴垂足为点H,
∵AB=
| 10 |
| 10 |
∵tan∠BAO=
| 1 |
| 3 |
| 1 |
| 3 |
∴∠BGH=∠BAO(1分)
∵∠BAO+∠ABO=90°,
∴∠BGH+∠ABO=90°,
∴∠GBA=90°,
∴∠ABQ=∠DOC=∠AOB(1分)
①当
| OD |
| OC |
| BQ |
| BA |
即
| 1 |
| 3 |
| BQ | ||
|
∴BQ=
| ||
| 3 |
过点Q作QN⊥y轴,垂足为点N,设Q(x,y),
∵
| NQ |
| BQ |
| HG |
| BG |
| |x| | ||||
|
| 1 | ||
|
| 1 |
| 3 |
| 1 |
| 3 |
∵tan∠GBH=
| 1 |
| 3 |
∴BN=1,
∴Q1(
| 1 |
| 3 |
| 1 |
| 3 |
②同理可得:Q3(3,10),Q4(-3,-8).(2分)
点评:此题主要考查了一次函数与坐标轴的交点问题、旋转变换及待定系数法求函数解析式及点的存在性问题,综合性很强,难度较大,要仔细对待.

练习册系列答案
相关题目
 ,对称轴是直线x=1,E为抛物线顶点.
,对称轴是直线x=1,E为抛物线顶点. (2013•门头沟区一模)已知关于x的一元二次方程
(2013•门头沟区一模)已知关于x的一元二次方程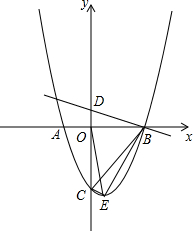 已知抛物线y=ax2-2x+c与x轴交于A(-1,0)、B两点,与y轴交于点C,对称轴为x=1,顶点为E,直线y=-
已知抛物线y=ax2-2x+c与x轴交于A(-1,0)、B两点,与y轴交于点C,对称轴为x=1,顶点为E,直线y=-