题目内容
 如图,已知A(2,0)、B(0,5),⊙C的圆心坐标为C(-1,0),半径为1,若D是⊙C上一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是________.
如图,已知A(2,0)、B(0,5),⊙C的圆心坐标为C(-1,0),半径为1,若D是⊙C上一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是________.
5-
分析:△ABE的BE边上高为OA=2,当AD与⊙C相切时,BE最短,此时,△ABE的面积最小,由勾股定理求相切时,AD的长,利用三角形相似求OE,再求BE,由三角形面积公式求面积的最小值.
解答: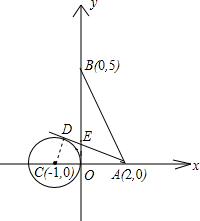 解:如图,当AD与⊙C相切于D点时,△ABE的面积最小,
解:如图,当AD与⊙C相切于D点时,△ABE的面积最小,
连接CD,则△ACD为直角三角形,
由勾股定理,得AD= =
= =2
=2 ,
,
∵∠CDA=∠EOA=90°,∠CAD=∠EAO,
∴△CAD∽△EAO,
∴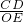 =
= ,即
,即 =
= ,解得OE=
,解得OE= ,
,
BE=OB-OE=5- ,
,
S△ABE= ×(5-
×(5- )×2=5-
)×2=5- .
.
故答案为:5- .
.
点评:本题考查了一次函数的综合运用.关键是根据动点的变化情况,找出使△ABE的面积最小时,D点的位置,利用相似比求OE.

分析:△ABE的BE边上高为OA=2,当AD与⊙C相切时,BE最短,此时,△ABE的面积最小,由勾股定理求相切时,AD的长,利用三角形相似求OE,再求BE,由三角形面积公式求面积的最小值.
解答:
 解:如图,当AD与⊙C相切于D点时,△ABE的面积最小,
解:如图,当AD与⊙C相切于D点时,△ABE的面积最小,连接CD,则△ACD为直角三角形,
由勾股定理,得AD=
 =
= =2
=2 ,
,∵∠CDA=∠EOA=90°,∠CAD=∠EAO,
∴△CAD∽△EAO,
∴
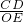 =
= ,即
,即 =
= ,解得OE=
,解得OE= ,
,BE=OB-OE=5-
 ,
,S△ABE=
 ×(5-
×(5- )×2=5-
)×2=5- .
.故答案为:5-
 .
.点评:本题考查了一次函数的综合运用.关键是根据动点的变化情况,找出使△ABE的面积最小时,D点的位置,利用相似比求OE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30° 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=