题目内容
如果两个多边形不仅相似(相似比不等于1),而且有一条公共边,那么就称这两个多边形是共边相似多边形.例如,图①中,△ABC与△ACD是共AC边相似三角形,图②中,□ABCD与□CEFD是共CD边相似四边形.
 |
(1)判断下列命题的真假(在相应括号内填上“真”或“假”):
①正三角形的共边相似三角形是正三角形.( )
②如果两个三角形是位似三角形,那么这两个三角形不可能是共边相似三角形.( )
(2)如图③,在△ABC中,∠C=90°,∠A=50°,画2个不全等的三角形,使这2个三角形均是与△ABC共BC边的相似三角形.(要求:画图工具不限,不写画法,保留画图痕迹或有必要的说明)
(3)图④是相邻两边长分别为a、b(a>b)的矩形,图⑤是边长为c的菱形,图⑥是两底长分别为d、e,腰长为f(0<e-d<2f)的等腰梯形,判断这三个图形是否存在共边相似四边形?如果存在,直接写出它们的共边相似四边形各边的长度.
 |
(4)根据(1)、(2)和(3)中获得的经验回答:如果一个多边形存在它的共边相似多边形,那么它必须满足条件: .
解:(1)①假.
②真.
(2)画图正确.
(3)该矩形存在共边相似四边形,各边长有两种情况,
分别是:① ,b,
,b, ,b;②
,b;② ,a,
,a, ,a.
,a.
该菱形不存在共边相似四边形.
该等腰梯形存在共边相似四边形,各边长有六种情况,
分别是:① ,d,
,d, ,
, ;②
;② ,
, ,d,d;③
,d,d;③ ,
, ,e,e;④e,
,e,e;④e, ,
, ,
, ;
;
⑤f, ,
, ,
, ;⑥
;⑥ ,f,
,f, ,
, .
.
(4)表述方法不唯一,如至少有两条边不相等,或各边长度不全相等,等等.

练习册系列答案
相关题目
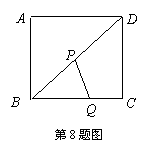
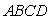 中有两个动点
中有两个动点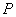 ,
, 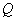 ,点
,点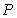 从点
从点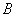 出发沿
出发沿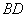 作匀速运动,到达点
作匀速运动,到达点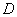 后停止;同时点
后停止;同时点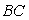 →
→ 作匀速运动,
作匀速运动,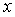 秒,两点之间的距离为
秒,两点之间的距离为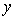 ,下列图象中,能表示
,下列图象中,能表示
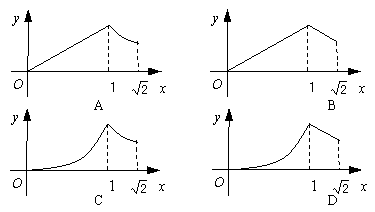


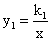 与
与 的图象相交于点A(1,2)和点B,当y1>y2时的变量x的取值范围是( )
的图象相交于点A(1,2)和点B,当y1>y2时的变量x的取值范围是( )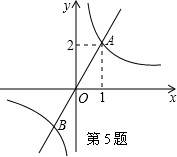
 2,x,0的平均数是0,那么这组数据的中位数是 。
2,x,0的平均数是0,那么这组数据的中位数是 。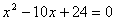 的两个解,且两圆的圆心距为d,若两圆相离,则下列结论正确的是( )
的两个解,且两圆的圆心距为d,若两圆相离,则下列结论正确的是( )  B.
B. C.
C. D.
D. 