题目内容
已知:如图,矩形 的两条对角线相交于点
的两条对角线相交于点 ,
,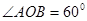 ,
, ,
, 平分
平分 交
交 于点
于点 .则
.则 的长为 ,
的长为 , 的长为 .
的长为 .
 的两条对角线相交于点
的两条对角线相交于点 ,
,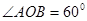 ,
, ,
, 平分
平分 交
交 于点
于点 .则
.则 的长为 ,
的长为 , 的长为 .
的长为 .
2;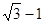
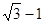
根据矩形的性质可知OA=OB,又因为∠AOB=60°,则OA=OB=AB=1,所以AC=2OA=2;由AE平分∠BAD,可得∠EAB=∠EAD,而AD∥BC,则∠EAD=∠AEB,故∠BAE=∠BEA,因此AB=BE=1,根据勾股AC2=AB2+BC2,可求得BC= 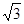 ,则EC="BC-BE="
,则EC="BC-BE=" 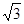 -1.
-1.
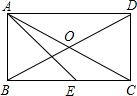
解:∵矩形ABCD
∴OA=OB
∵∠AOB="60°"
∴OA=OB=AB=1
∴AC=2OA=2
∵AE平分∠BAD
∴∠EAB=∠EAD
∵AD∥BC
∴∠EAD=∠AEB
∴∠BAE=∠BEA
∴AB=BE=1
∵AC2=AB2+BC2
∴BC=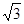
∴EC=BC-BE=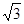 -1.
-1.
故答案为2,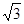 -1.
-1.
根据矩形的性质,结合勾股定理求解.
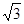 ,则EC="BC-BE="
,则EC="BC-BE=" 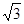 -1.
-1.
解:∵矩形ABCD
∴OA=OB
∵∠AOB="60°"
∴OA=OB=AB=1
∴AC=2OA=2
∵AE平分∠BAD
∴∠EAB=∠EAD
∵AD∥BC
∴∠EAD=∠AEB
∴∠BAE=∠BEA
∴AB=BE=1
∵AC2=AB2+BC2
∴BC=
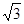
∴EC=BC-BE=
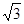 -1.
-1.故答案为2,
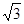 -1.
-1.根据矩形的性质,结合勾股定理求解.

练习册系列答案
相关题目
 中,
中, 平分
平分 分别为AD、AB中点,点G为BC边上一点,且
分别为AD、AB中点,点G为BC边上一点,且
 ;
; 时,四边形
时,四边形 为平行
为平行 四边形,并说明理由.
四边形,并说明理由.

 、正方形
、正方形 和正方形
和正方形 的位置如图所示,点
的位置如图所示,点 在线段
在线段 上,正方形
上,正方形 的面积为( )
的面积为( )

 ,则
,则
 ,则
,则
 中,
中, ,
, ,
, ,
, ,则
,则 ( )
( )





 的正六边形.如果用一个含
的正六边形.如果用一个含 角的直角三角板的角,借助点
角的直角三角板的角,借助点 等分,那么
等分,那么