题目内容
如图,△ABP中,∠APB=∠α,把△ABP绕点A逆时针旋转60°后得到△ACE.连结BC、PE、PC,测量得∠BPC=100°.
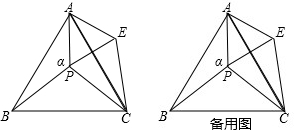
(1)请找出图中的两个等边三角形:______ (不再添加其它点或线)
(2)若∠α=150°,试判断△PEC的形状,并说明你的理由;
(3)若△CPE为等腰三角形,求∠α的度数.
解:(1)∵△ABP绕点A逆时针旋转60°后得到△ACE,
∴∠BAC=∠PAE=60°,AB=AC,AP=AE,
∴△ABC和△APE都是等边三角形;
故答案为△ABC,△APE;
(2)∵△APE是等边三角形,
∴∠APE=∠AEP=60°,
∵△ABP绕点A逆时针旋转60°后得到△ACE,
∴∠AEC=∠APB=150°,
∴∠CEP=∠AEC-∠AEP=150°-60°=90°,
又∵∠CPE=360°-∠APB-∠BPC-∠APE=50°,
∴△PEC是直角三角形;
(3)∵∠CPE=360°-∠APB-∠BPC-∠APE=200°-α,
而∠CEP=∠AEC-∠AEP=α-60°,
∴∠PCE=180°-∠CPE-∠CEP=180°-(200°-α)-(α-60°)=40°,
∵△CPE为等腰三角形,下面分三种情况讨论:
①当∠CPE=∠CEP时,
200°-α=α-60°,解得α=130°;
②当∠CPE=∠PCE时,
200°-α=40°,解得α=160°;
③当∠PCE=∠CEP时,α-60°=40°,解得α=100°…
综上所述,若△CPE为等腰三角形,则α=100°,130°,160°.
分析:(1)根据旋转的性质得到∠BAC=∠PAE=60°,AB=AC,AP=AE,然后根据等边三角形的判定方法可确定△ABC和△APE都是等边三角形;
(2)根据等边三角形的性质由△APE是等边三角形得到∠APE=∠AEP=60°,再利用旋转的性质得∠AEC=∠APB=150°,则可计算出∠CEP=90°,∠CPE=50°,于是可判断△PEC是直角三角形;
(3)先用α表示∠CPE=200°-α,∠CEP=α-60°,再利用三角形内角和定理计算出∠PCE=40°,然后由△CPE为等腰三角形分类讨论:当∠CPE=∠CEP时,即200°-α=α-60°;当∠CPE=∠PCE时,即200°-α=40°;当∠PCE=∠CEP时,即α-60°=40°,再分别解方程求α.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的判定与性质以及等腰三角形的性质.
∴∠BAC=∠PAE=60°,AB=AC,AP=AE,
∴△ABC和△APE都是等边三角形;
故答案为△ABC,△APE;
(2)∵△APE是等边三角形,
∴∠APE=∠AEP=60°,
∵△ABP绕点A逆时针旋转60°后得到△ACE,
∴∠AEC=∠APB=150°,
∴∠CEP=∠AEC-∠AEP=150°-60°=90°,
又∵∠CPE=360°-∠APB-∠BPC-∠APE=50°,
∴△PEC是直角三角形;
(3)∵∠CPE=360°-∠APB-∠BPC-∠APE=200°-α,
而∠CEP=∠AEC-∠AEP=α-60°,
∴∠PCE=180°-∠CPE-∠CEP=180°-(200°-α)-(α-60°)=40°,
∵△CPE为等腰三角形,下面分三种情况讨论:
①当∠CPE=∠CEP时,
200°-α=α-60°,解得α=130°;
②当∠CPE=∠PCE时,
200°-α=40°,解得α=160°;
③当∠PCE=∠CEP时,α-60°=40°,解得α=100°…
综上所述,若△CPE为等腰三角形,则α=100°,130°,160°.
分析:(1)根据旋转的性质得到∠BAC=∠PAE=60°,AB=AC,AP=AE,然后根据等边三角形的判定方法可确定△ABC和△APE都是等边三角形;
(2)根据等边三角形的性质由△APE是等边三角形得到∠APE=∠AEP=60°,再利用旋转的性质得∠AEC=∠APB=150°,则可计算出∠CEP=90°,∠CPE=50°,于是可判断△PEC是直角三角形;
(3)先用α表示∠CPE=200°-α,∠CEP=α-60°,再利用三角形内角和定理计算出∠PCE=40°,然后由△CPE为等腰三角形分类讨论:当∠CPE=∠CEP时,即200°-α=α-60°;当∠CPE=∠PCE时,即200°-α=40°;当∠PCE=∠CEP时,即α-60°=40°,再分别解方程求α.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的判定与性质以及等腰三角形的性质.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
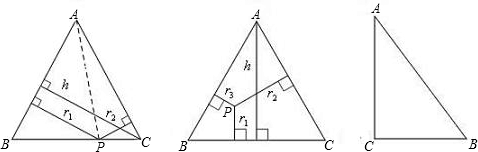

 如图,△ABP中,∠APB=120°,点C、D在线段AB上,△PCD是等边三角形,请根据所述条件,判断下列论断:①CD2=AC•DB;②AP2=AC•AB;③AP•PC=PD•PB;④BP2-BD2=AD•DB,其中正确的个数是( )
如图,△ABP中,∠APB=120°,点C、D在线段AB上,△PCD是等边三角形,请根据所述条件,判断下列论断:①CD2=AC•DB;②AP2=AC•AB;③AP•PC=PD•PB;④BP2-BD2=AD•DB,其中正确的个数是( ) 如图,△ABP中,∠APB=120°,点C、D在线段AB上,△PCD是等边三角形,请根据所述条件,判断下列论断:①CD2=AC•DB;②AP2=AC•AB;③AP•PC=PD•PB;④BP2-BD2=AD•DB,其中正确的个数是
如图,△ABP中,∠APB=120°,点C、D在线段AB上,△PCD是等边三角形,请根据所述条件,判断下列论断:①CD2=AC•DB;②AP2=AC•AB;③AP•PC=PD•PB;④BP2-BD2=AD•DB,其中正确的个数是