题目内容
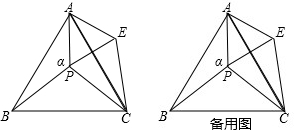
 如图,△ABP中,∠APB=120°,点C、D在线段AB上,△PCD是等边三角形,请根据所述条件,判断下列论断:①CD2=AC•DB;②AP2=AC•AB;③AP•PC=PD•PB;④BP2-BD2=AD•DB,其中正确的个数是
如图,△ABP中,∠APB=120°,点C、D在线段AB上,△PCD是等边三角形,请根据所述条件,判断下列论断:①CD2=AC•DB;②AP2=AC•AB;③AP•PC=PD•PB;④BP2-BD2=AD•DB,其中正确的个数是
- A.4
- B.3
- C.2
- D.1
B
分析:由△ABP中,∠APB=120°,点C、D在线段AB上,△PCD是等边三角形,易证得△APC∽△PBD∽△ABP,然后由相似三角形的对应边成比例,可证得:①CD2=AC•DB;②AP2=AC•AB正确,③AP•PC=PD•PB错误,可得BP2-BD2=AB•BD-BD2=BD•(AB-BD)=AD•DB,即④正确.
解答:∵△PCD是等边三角形,
∴∠CPD=∠PCD=∠PDC=60°,PC=PD=CD,
∴∠ACP=∠PDB=120°,∠A+∠APC=∠PCD=60°,
∵∠APB=120°,
∴∠A+∠B=180°-∠APB=60°,
∴∠APC=∠B,
∴△APC∽△PBD,
∴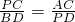 ,
,
∴PC•PD=AC•DB,
∴CD2=AC•DB;
故①正确;
∵∠APC=∠B,∠A是公共角,
∴△APC∽△ABP,
∴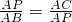 ,
,
∴AP2=AC•AB;
故②正确;
∵△APC∽△PBD,
∴AP:PB=PC:BD,
∴AP•BD=PC•PB,
∵PC=PD=CD,
∴AP•BD=PD•PB,
故③错误;
∵△APC∽△PBD,△APC∽△ABP,
∴△PBD∽△ABP,
∴BP:AB=BD:BP,
∴BP2=AB•BD,
∴BP2-BD2=AB•BD-BD2=BD•(AB-BD)=AD•DB;
故④正确.
故选B.
点评:此题考查了相似三角形的判定与性质以及等边三角形的性质.此题难度较大,注意掌握数形结合思想的应用.
分析:由△ABP中,∠APB=120°,点C、D在线段AB上,△PCD是等边三角形,易证得△APC∽△PBD∽△ABP,然后由相似三角形的对应边成比例,可证得:①CD2=AC•DB;②AP2=AC•AB正确,③AP•PC=PD•PB错误,可得BP2-BD2=AB•BD-BD2=BD•(AB-BD)=AD•DB,即④正确.
解答:∵△PCD是等边三角形,
∴∠CPD=∠PCD=∠PDC=60°,PC=PD=CD,
∴∠ACP=∠PDB=120°,∠A+∠APC=∠PCD=60°,
∵∠APB=120°,
∴∠A+∠B=180°-∠APB=60°,
∴∠APC=∠B,
∴△APC∽△PBD,
∴
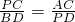 ,
,∴PC•PD=AC•DB,
∴CD2=AC•DB;
故①正确;
∵∠APC=∠B,∠A是公共角,
∴△APC∽△ABP,
∴
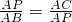 ,
,∴AP2=AC•AB;
故②正确;
∵△APC∽△PBD,
∴AP:PB=PC:BD,
∴AP•BD=PC•PB,
∵PC=PD=CD,
∴AP•BD=PD•PB,
故③错误;
∵△APC∽△PBD,△APC∽△ABP,
∴△PBD∽△ABP,
∴BP:AB=BD:BP,
∴BP2=AB•BD,
∴BP2-BD2=AB•BD-BD2=BD•(AB-BD)=AD•DB;
故④正确.
故选B.
点评:此题考查了相似三角形的判定与性质以及等边三角形的性质.此题难度较大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
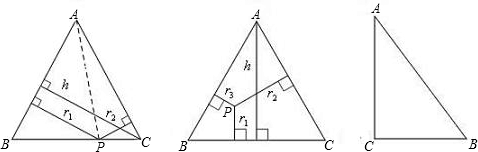

 如图,△ABP中,∠APB=120°,点C、D在线段AB上,△PCD是等边三角形,请根据所述条件,判断下列论断:①CD2=AC•DB;②AP2=AC•AB;③AP•PC=PD•PB;④BP2-BD2=AD•DB,其中正确的个数是( )
如图,△ABP中,∠APB=120°,点C、D在线段AB上,△PCD是等边三角形,请根据所述条件,判断下列论断:①CD2=AC•DB;②AP2=AC•AB;③AP•PC=PD•PB;④BP2-BD2=AD•DB,其中正确的个数是( )