题目内容

如图，已知A（n，-2），B（1，4）是一次函数y=kx+b的图象和反比例函数y= $数学公式$ 的图象的两个交点，直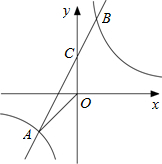线AB与y轴交于点C．
（1）求反比例函数和一次函数的关系式；
（2）求△AOC的面积；
（3）求不等式kx+b- $数学公式$ ＜0的解集．（直接写出答案）

解：（1）∵B（1，4）在反比例函数y= $\text{[math]}$ 上，
∴m=4，
又∵A（n，-2）在反比例函数y= $\text{[math]}$ 的图象上，
∴n=-2，
又∵A（-2，-2），B（1，4）是一次函数y=kx+b的上的点，联立方程组解得，
k=2，b=2，
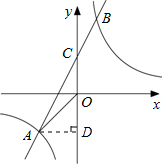
∴ $\text{[math]}$ ，y=2x+2；

（2）过点A作AD⊥CD，
∵一次函数y=kx+b的图象和反比例函数y= $\text{[math]}$ 的图象的两个交点为A，B，联立方程组解得，
A（-2，-2），B（1，4），C（0，2），
∴AD=2，CO=2，
∴△AOC的面积为：S= $\text{[math]}$ AD•CO= $\text{[math]}$ ×2×2=2；

（3）由图象知：当0＜x＜1和-2＜x＜0时函数y= $\text{[math]}$ 的图象在一次函数y=kx+b图象的上方，
∴不等式kx+b- $\text{[math]}$ ＜0的解集为：0＜x＜1或x＜-2．
分析：（1）由B点在反比例函数y= $\text{[math]}$ 上，可求出m，再由A点在函数图象上，由待定系数法求出函数解析式；
（2）由上问求出的函数解析式联立方程求出A，B，C三点的坐标，从而求出△AOC的面积；
（3）由图象观察函数y= $\text{[math]}$ 的图象在一次函数y=kx+b图象的上方，对应的x的范围．
点评：此题考查一次函数和反比例函数的性质及图象，考查用待定系数法求函数的解析式，还间接考查函数的增减性，从而来解不等式．