题目内容
4.先化简,再求值:($\frac{{x}^{2}-y}{x}$-x-1)÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-2xy+{y}^{2}}$,其中x=$\sqrt{5}$,y=$\sqrt{10}$.分析 先算括号内的加法,同时把除法变成乘法,再算乘法,最后代入求出即可.
解答 解:($\frac{{x}^{2}-y}{x}$-x-1)÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-2xy+{y}^{2}}$
=$\frac{{x}^{2}-y-x(x+1)}{x}$•$\frac{(x-y)^{2}}{(x+y)(x-y)}$
=-$\frac{x+y}{x}$•$\frac{x-y}{x+y}$
=-$\frac{x-y}{x}$
把$x=\sqrt{5},\;y=\sqrt{10}$代入得 原式=$\frac{\sqrt{5}-\sqrt{10}}{\sqrt{5}}$=$\sqrt{2}$-1.
点评 本题考查了分式的混合运算和求值,能正确根据分式的运用法则进行化简是解此题的关键,注意运算顺序.

练习册系列答案
相关题目
14.某校12名学生参加区级诗词大赛,他们得分情况如下表所示:
则这12名学生所得分数的众数是90分.
| 分数 | 87 | 88 | 90 | 93 | 97 |
| 人数 | 2 | 3 | 4 | 2 | 1 |
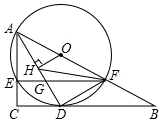 如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
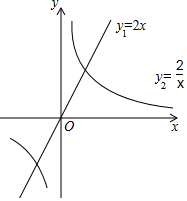 在平面直角坐标系xOy中,直线y1=2x与双曲线y2=$\frac{2}{x}$ 的图象如图所示,小明说:“满足y1>y2的x的取值范围是x>1.”你同意他的观点吗?答:不同意.理由是y1>y2的x的取值范围是x>1或-1<x<0.
在平面直角坐标系xOy中,直线y1=2x与双曲线y2=$\frac{2}{x}$ 的图象如图所示,小明说:“满足y1>y2的x的取值范围是x>1.”你同意他的观点吗?答:不同意.理由是y1>y2的x的取值范围是x>1或-1<x<0.