题目内容
如图,已知在平面直角坐标系xoy中,一次函数y=kx+b(k≠0)的图象与反比例函数y= (m≠0)的图
(m≠0)的图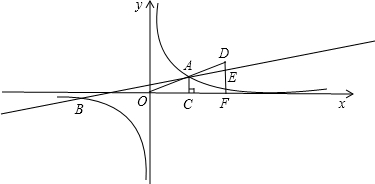 象交于A、B两点,且点B的纵坐标为
象交于A、B两点,且点B的纵坐标为 ,过点A作AC⊥x轴于点C,AC=1,OC=2.
,过点A作AC⊥x轴于点C,AC=1,OC=2.
(1)求反比例函数和一次函数解析式;
(2)连接OA,并延长OA到点D,使AD=OA,作DF⊥x轴,F为垂足,交反比例函数图象于点E,求点E的坐标.
解:(1)∵AC=1,OC=2,
∴点A的坐标为(2,1),
∵反比例函数y= 的图象经过点A(2,1),
的图象经过点A(2,1),
∴m=2,
∴反比例函数的解析式为y= ,
,
∵反比例函数y= 的图象经过点B且点B的纵坐标为-
的图象经过点B且点B的纵坐标为- ,
,
∴点B的坐标为(-4,- ),
),
∵一次函数y=kx+b的图象经过点A(2,1)点B(-4,- ),
),
∴ ,
,
解得:k= ,b=
,b= ,
,
故一次函数的解析式为y= x+
x+ ;
;
(2)∵AC⊥x轴,DF⊥x轴,
∴AC∥DF,
∴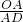 =
= ,
,
∵AD=OA,
∴OC=CF,
∵OC=2,
∴CF=2,
∴点F的横坐标为4,
∴点E的横坐标也为4,
∴y= =
= .
.
故点E的坐标为(4, ).
).
分析:(1)根据已知得出点A的坐标,再根据反比例函数y= 的图象经过点A(2,1),求出m的值,得出反比例函数的解析式,从而求出点B的坐标,再根据一次函数y=kx+b的图象经过点A和点B,求出k和b的值,得出一次函数的解析式;
的图象经过点A(2,1),求出m的值,得出反比例函数的解析式,从而求出点B的坐标,再根据一次函数y=kx+b的图象经过点A和点B,求出k和b的值,得出一次函数的解析式;
(2)根据AC⊥x轴,DF⊥x轴,得出AC∥DF,即可得出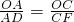 ,根据AD=OA,求出OC=CF=2,得出点F的横坐标,从而得出点E的坐标.
,根据AD=OA,求出OC=CF=2,得出点F的横坐标,从而得出点E的坐标.
点评:此题考查了反比例函数的综合,解题的关键是根据所给的条件得出A、B点的坐标,求出函数的解析式.注意运用数形结合的思想,难度不大,是中考常考的题型.
∴点A的坐标为(2,1),
∵反比例函数y=
 的图象经过点A(2,1),
的图象经过点A(2,1),∴m=2,
∴反比例函数的解析式为y=
 ,
,∵反比例函数y=
 的图象经过点B且点B的纵坐标为-
的图象经过点B且点B的纵坐标为- ,
,∴点B的坐标为(-4,-
 ),
),∵一次函数y=kx+b的图象经过点A(2,1)点B(-4,-
 ),
),∴
 ,
,解得:k=
 ,b=
,b= ,
,故一次函数的解析式为y=
 x+
x+ ;
;(2)∵AC⊥x轴,DF⊥x轴,
∴AC∥DF,
∴
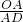 =
= ,
,∵AD=OA,
∴OC=CF,
∵OC=2,
∴CF=2,
∴点F的横坐标为4,
∴点E的横坐标也为4,
∴y=
 =
= .
.故点E的坐标为(4,
 ).
).分析:(1)根据已知得出点A的坐标,再根据反比例函数y=
 的图象经过点A(2,1),求出m的值,得出反比例函数的解析式,从而求出点B的坐标,再根据一次函数y=kx+b的图象经过点A和点B,求出k和b的值,得出一次函数的解析式;
的图象经过点A(2,1),求出m的值,得出反比例函数的解析式,从而求出点B的坐标,再根据一次函数y=kx+b的图象经过点A和点B,求出k和b的值,得出一次函数的解析式;(2)根据AC⊥x轴,DF⊥x轴,得出AC∥DF,即可得出
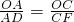 ,根据AD=OA,求出OC=CF=2,得出点F的横坐标,从而得出点E的坐标.
,根据AD=OA,求出OC=CF=2,得出点F的横坐标,从而得出点E的坐标.点评:此题考查了反比例函数的综合,解题的关键是根据所给的条件得出A、B点的坐标,求出函数的解析式.注意运用数形结合的思想,难度不大,是中考常考的题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),
如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),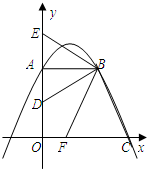 边分别交y轴的正半轴、x轴的正半轴于点E和F.
边分别交y轴的正半轴、x轴的正半轴于点E和F.
 (2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=
(2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2= 如图,已知在平面直角坐标系中,△ABC的位置如图所示
如图,已知在平面直角坐标系中,△ABC的位置如图所示