Question

【题目】如图，在平面直角坐标系中，点，射线轴，直线交线段于点，交轴于点，是射线上一点．若存在点，使得恰为等腰直角三角形，则的值为_______.

Answer 1

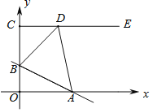
【答案】3或6

【解析】

先表示出A、B坐标，分①当∠ABD=90°时，②当∠ADB=90°时，③当∠DAB=90°时，建立等式解出b即可.

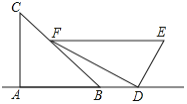
解：①当∠ABD=90°时，如图1，则∠DBC+∠ABO=90°，,

∴∠DBC=∠BAO，

由直线交线段OC于点B，交x轴于点A可知OB=b，OA=b，

∵点C（0，6），

∴OC=6，

∴BC=6-b，

在△DBC和△BAO中，

∴△DBC≌△BAO（AAS），

∴BC=OA，

即6-b=b，

∴b=3；

②当∠ADB=90°时，如图2，作AF⊥CE于F，

同理证得△BDC≌△DAF，

∴CD=AF=6，BC=DF，

∵OB=b，OA=b，

∴BC=DF=b-6，

∵BC=6-b，

∴6-b=b-6，

∴b=6；

③当∠DAB=90°时，如图3，

作DF⊥OA于F，

同理证得△AOB≌△DFA，

∴OA=DF，

∴b=6；

综上，b的值为3或6，

故答案为3或6.