题目内容
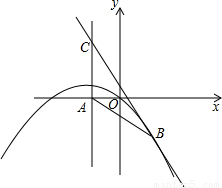
 如图,抛物线经过原点O、点A(6,8)和点(3,-5).
如图,抛物线经过原点O、点A(6,8)和点(3,-5).(1)求直线OA的表达式;
(2)求抛物线的表达式;
(3)如果点B在线段OA上,与y轴平行的直线BC与抛物线相交于点C,△OBC是等腰三角形,求点C的坐标?
分析:(1)设直线OA的表达式y=kx,把A的坐标代入求出k即可;
(2)设抛物线的表达为y=ax2+bx,把A的坐标和(3,-5)代入得到方程组,求出方程组的解即可;
(3)设直线BC与x轴相交于点H,设B(3m,4m),得出OH=3m,BH=4m,OB=5m,当OC=OB时,得出方程-4m=9m2-14m,当BC=OB=5m时,得出方程-m=9m2-14m,当BC=OC时,过点C作CE⊥OB,垂足为E,得到方程
m=9m2-14m,求出方程的解即可得到C的坐标.
(2)设抛物线的表达为y=ax2+bx,把A的坐标和(3,-5)代入得到方程组,求出方程组的解即可;
(3)设直线BC与x轴相交于点H,设B(3m,4m),得出OH=3m,BH=4m,OB=5m,当OC=OB时,得出方程-4m=9m2-14m,当BC=OB=5m时,得出方程-m=9m2-14m,当BC=OC时,过点C作CE⊥OB,垂足为E,得到方程
| 7 |
| 8 |
解答:解:(1)设直线OA的表达式y=kx,
∵A(6,8),
∴8=6k,
解得k=
,
∴所求直线的表达式为y=
x,
答:直线OA的表达式为y=
x.
(2)设抛物线的表达为y=ax2+bx,
∵抛物线经过点(6,8)、(3,-5),
∴
,
解得
,
∴所求抛物线的表达式为y=x2-
x,
答:抛物线的表达式为y=x2-
x.
(3)设直线BC与x轴相交于点H,
∵BC∥y轴,
∴BC⊥x轴,
设B(3m,4m),
则OH=3m,BH=4m,OB=5m,
由于△OBC是等腰三角形,
所以当OC=OB时,CH=BH=4m,点C(3m,-4m),
∴-4m=9m2-14m,
∴m1=0(舍去),m2=
,
∴C(
,-
);
当BC=OB=5m时,CH=BC-BH=m,点C(3m,-m),
∴-m=9m2-14m,
∴m1=0(舍去),m2=
,
∴C(
,-
);
当BC=OC时,过点C作CE⊥OB,垂足为E,BE=
OB=
m,
BC=
=
=
m,CH=BH-BC=4m-
m=
m,
点C(3m,
m),
∴
m=9m2-14m,
∴m1=0(舍去),m2=
,
∴C(
,
),
答:点C的坐标为(
,-
)或(
,-
)或(
,
).
∵A(6,8),
∴8=6k,
解得k=
| 4 |
| 3 |
∴所求直线的表达式为y=
| 4 |
| 3 |
答:直线OA的表达式为y=
| 4 |
| 3 |
(2)设抛物线的表达为y=ax2+bx,
∵抛物线经过点(6,8)、(3,-5),
∴
|
解得
|

∴所求抛物线的表达式为y=x2-
| 14 |
| 3 |
答:抛物线的表达式为y=x2-
| 14 |
| 3 |
(3)设直线BC与x轴相交于点H,
∵BC∥y轴,
∴BC⊥x轴,
设B(3m,4m),
则OH=3m,BH=4m,OB=5m,
由于△OBC是等腰三角形,
所以当OC=OB时,CH=BH=4m,点C(3m,-4m),
∴-4m=9m2-14m,
∴m1=0(舍去),m2=
| 10 |
| 9 |
∴C(
| 10 |
| 3 |
| 40 |
| 9 |
当BC=OB=5m时,CH=BC-BH=m,点C(3m,-m),
∴-m=9m2-14m,
∴m1=0(舍去),m2=
| 13 |
| 9 |
∴C(
| 13 |
| 3 |
| 13 |
| 9 |
当BC=OC时,过点C作CE⊥OB,垂足为E,BE=
| 1 |
| 2 |
| 5 |
| 2 |
BC=
| BE |
| cos∠OBH |
| ||
|
| 25 |
| 8 |
| 25 |
| 8 |
| 7 |
| 8 |
点C(3m,
| 7 |
| 8 |
∴
| 7 |
| 8 |
∴m1=0(舍去),m2=
| 119 |
| 24 |
∴C(
| 119 |
| 24 |
| 833 |
| 576 |
答:点C的坐标为(
| 10 |
| 3 |
| 40 |
| 9 |
| 13 |
| 3 |
| 13 |
| 9 |
| 119 |
| 24 |
| 833 |
| 576 |
点评:本题主要考查对用待定系数法求一次函数、二次函数的解析式,解一元二次方程,解二元一次方程组,等腰三角形的性质,勾股定理等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 A,直线y=-2x+1与抛物线交于点B,且与y轴、直线x=-2分别交于点D、C.
A,直线y=-2x+1与抛物线交于点B,且与y轴、直线x=-2分别交于点D、C.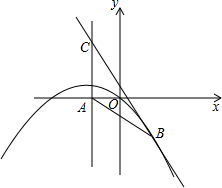 A,直线y=-2x+1与抛物线交于点B,且与y轴、直线x=-2分别交于点D、C.
A,直线y=-2x+1与抛物线交于点B,且与y轴、直线x=-2分别交于点D、C.