题目内容
 如图,小明在大楼45米高(即PH=45米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:
如图,小明在大楼45米高(即PH=45米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:| 3 |
(1)山坡坡脚(即∠ABC)的度数等于
(2)求A、B两点间的距离.(结果精确到1米,参考数据:
| 3 |
考点:解直角三角形的应用-仰角俯角问题,解直角三角形的应用-坡度坡角问题
专题:
分析:(1)根据俯角以及坡度的定义即可求解;
(2)在直角△PHB中,根据三角函数即可求得PB的长,然后利用直角△PBA为等腰直角三角形,即可求解.
(2)在直角△PHB中,根据三角函数即可求得PB的长,然后利用直角△PBA为等腰直角三角形,即可求解.
解答:解:(1)∵tan∠ABC=1:
,
∴∠ABC=30°;
故答案为:30;
(2)由题意得:∠PBH=60°,
∵∠ABC=30°,
∴∠ABP=90°,又∠APB=45°,
∴△PAB为等腰直角三角形,
在直角△PHB中,PB=
=
=30
,
在直角△PBA中,AB=PB=30
≈52米.
| 3 |
∴∠ABC=30°;
故答案为:30;
(2)由题意得:∠PBH=60°,
∵∠ABC=30°,
∴∠ABP=90°,又∠APB=45°,
∴△PAB为等腰直角三角形,
在直角△PHB中,PB=
| PH |
| sin∠PBH |
| 45 | ||||
|
| 3 |
在直角△PBA中,AB=PB=30
| 3 |
点评:此题考查了解直角三角形的应用,用到的知识点是俯角的定义以及坡度坡角的知识,注意能借助俯角构造直角三角形并解直角三角形是关键,注意数形结合思想的应用.

练习册系列答案
相关题目

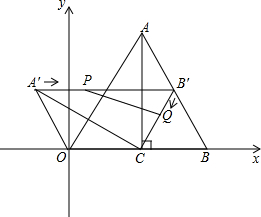 如图,在平面直角坐标系中,Rt△AOC的顶点O在坐标原点,直角顶点C在x轴的正半轴上,顶点A在第一象限.以AC为轴将△AOC翻折得到△ACB,然后将△ACB绕点C逆时针旋转60°,得到△A′CB′.已知OA=4cm,∠OAC=30°.
如图,在平面直角坐标系中,Rt△AOC的顶点O在坐标原点,直角顶点C在x轴的正半轴上,顶点A在第一象限.以AC为轴将△AOC翻折得到△ACB,然后将△ACB绕点C逆时针旋转60°,得到△A′CB′.已知OA=4cm,∠OAC=30°.