Question

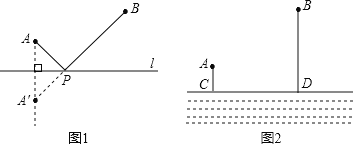
【题目】如图所示，四边形是正方形， 是延长线上一点．直角三角尺的一条直角边经过点，且直角顶点在边上滑动(点不与点重合)，另一直角边与的平分线相交于点．

(1)求证: ;

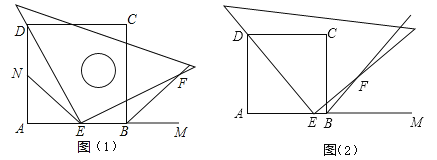
(2)如图(1)，当点在边的中点位置时，猜想与的数量关系，并证明你的猜想;

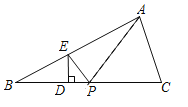
(3)如图(2)，当点在边(除两端点)上的任意位置时，猜想此时与有怎样的数量关系，并证明你的猜想．

Answer 1

【答案】（1）详见解析；（2），理由详见解析；（3），理由详见解析

【解析】

（1）根据，等量代换即可证明；（2）DE=EF，连接NE，在DA边上截取DN=EB，证出△DNE≌△EBF即可得出答案；（3）在边上截取，连接，证出即可得出答案．

(1)证明:∵，

∴，

∴;

(2) 理由如下:

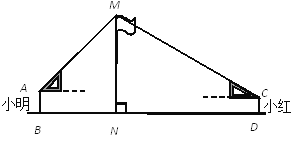
如图，取的中点，连接，

∵四边形为正方形，

∴ ，

∵分别为中点

∴，

∴

又∵

∴

∴，

又∵，平分

∴．

∴

在和中

，

∴

(3) .理由如下:

如图，在边上截取，连接，

∵四边形是正方形， ，

∴，

∴为等腰直角三角形，

∵

∴，

∵平分， ，

∴，

∴，

在和中

∴，

∴．