题目内容
如图，设△ABC为等腰三角形，AC=BC，P为△ABC外接圆上任意一点，且P与C在弦AB的异侧．求证：| PA+PB |
| PC |
| AB |
| AC |
分析：延长AP至D，使PB=PD，则AP+PD=AD，由圆周角定理可得∠APC=∠BPC，再根据PB=PD，∠PAB=∠PCB，即可得到△CPB∽△ADB，由相似三角形的对应边成比例即可求出答案．
解答：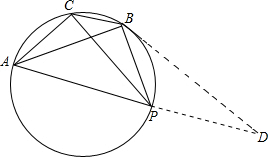
解：延长AP至D，使PB=PD，连接BD，则AP+PD=AD，
∵AC=BC，
∴∠APC=∠BPC，
∵PB=PD，
∴∠BPC=
∠BPA=∠D，
又∵∠PAB=∠PCB，
∴△CPB∽△ADB，
∴
=
，
∴
=
=
．
解：延长AP至D，使PB=PD，连接BD，则AP+PD=AD，∵AC=BC，
∴∠APC=∠BPC，
∵PB=PD，
∴∠BPC=
| 1 |
| 2 |
又∵∠PAB=∠PCB，
∴△CPB∽△ADB，
∴
| PC |
| AD |
| BC |
| AB |
∴
| PA+PB |
| PC |
| AB |
| BC |
| AB |
| AC |
点评：本题考查的是圆周角定理及相似三角形的判定与性质，能根据题意作出辅助线，构造出相似三角形是解答此题的关键．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
如图，设P到等边三角形ABC两顶点A、B的距离分别为2、3，则PC所能达到的最大值为（ ）
A、
| ||
B、
| ||
| C、5 | ||
| D、6 |
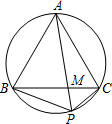如图，点P为等边△ABC外接圆劣弧BC上一点．
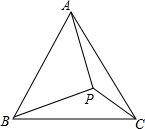如图，设P为等边△ABC内一点，且PA=4，PB=5，PC=3．则△ABC的边长为________．