题目内容
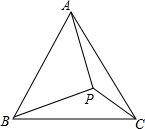 如图,设P为等边△ABC内一点,且PA=4,PB=5,PC=3.则△ABC的边长为________.
如图,设P为等边△ABC内一点,且PA=4,PB=5,PC=3.则△ABC的边长为________.
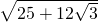
分析:首先将△BCP绕点C顺时针旋转60°得△ACQ,连接PQ.再过A作CP的延长线的垂线AD,垂足为D,易证得△PCQ是等边三角形,△APQ是直角三角形,则可求得∠APC的度数,然后可求得∠APD的度数,在Rt△APD中,即可求得AD与CD的长,继而求得AC.
解答:
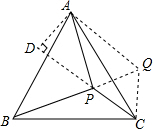 解:将△BCP绕点C顺时针旋转60°得△ACQ,连接PQ.再过A作CP的延长线的垂线AD,垂足为D,
解:将△BCP绕点C顺时针旋转60°得△ACQ,连接PQ.再过A作CP的延长线的垂线AD,垂足为D,∴AQ=PB=5,CQ=PC,∠PCQ=60°,
∴△PCQ是等边三角形,
∴PQ=PC=3,∠QPC=60°,
在△PAQ中,∵PA=4,AQ=5,PQ=3,
∴AQ2=PA2+PQ2,
∴∠APQ=90°,
∴∠APC=∠APQ+∠QPC=150°,
∴∠APD=30°,
在Rt△APD中,AD=
 PA=2,PD=AP•cos30°=2
PA=2,PD=AP•cos30°=2 ,
,则CD=PC+PD=3+2
 ,
,在Rt△ACD中,AC2=AD2+CD2=4+(3+2
 )2=25+12
)2=25+12 ,则AC=
,则AC=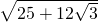 .
.故答案是:
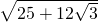 .
.点评:此题考查了等边三角形的判定与性质、勾股定理的逆定理以及直角三角形的性质.此题难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
如图,设P到等边三角形ABC两顶点A、B的距离分别为2、3,则PC所能达到的最大值为( )

A、
| ||
B、
| ||
| C、5 | ||
| D、6 |
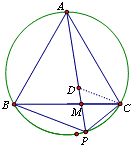
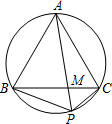 如图,点P为等边△ABC外接圆劣弧BC上一点.
如图,点P为等边△ABC外接圆劣弧BC上一点.