题目内容
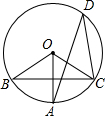如图，BC是⊙O的弦，OA⊥BC，∠AOB=70°，则∠ADC的度数是（ ）| A、70° | B、35° | C、45° | D、60° |
分析：欲求∠ADC，又已知一圆心角，可利用圆周角与圆心角的关系求解．
解答：解：∵A、B、C、D是⊙O上的四点，OA⊥BC，
∴弧AC=弧AB （垂径定理），
∴∠ADC=
∠AOB（等弧所对的圆周角是圆心角的一半）；
又∠AOB=70°，
∴∠ADC=35°．
故选B．
∴弧AC=弧AB （垂径定理），
∴∠ADC=
| 1 |
| 2 |
又∠AOB=70°，
∴∠ADC=35°．
故选B．
点评：本题考查垂径定理、圆周角定理．关键是将证明弧相等的问题转化为证明所对的圆心角相等．
练习册系列答案
相关题目
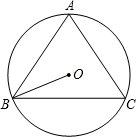已知：如图，BC是⊙O的弦，点A在⊙O上，AB=AC=10，
17、如图，BC是⊙O的弦，圆周角∠BAC=50°，则∠OCB的度数是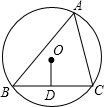
如图，BC是⊙O的弦，A是⊙O上一点，OD⊥BC于D，且BD=
如图，BC是⊙O的弦，OD⊥BC于E，交