题目内容
【题目】定义:已知点![]() 是三角形边上的一点(顶点除外),若它到三角形一条边的距离等于它到三角形的一个顶点的距离,则我们把点
是三角形边上的一点(顶点除外),若它到三角形一条边的距离等于它到三角形的一个顶点的距离,则我们把点![]() 叫做该三角形的等距点.
叫做该三角形的等距点.
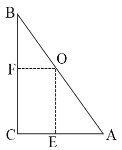
(1)如图1:![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在斜边
在斜边![]() 上,且点
上,且点![]() 是
是![]() 的等距点,试求
的等距点,试求![]() 的长;
的长;
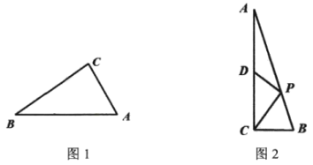
(2)如图2,![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() 为
为![]() 中点,且
中点,且![]() .
.
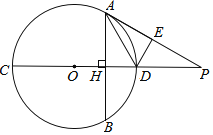
①求证:![]() 的外接圆圆心是
的外接圆圆心是![]() 的等距点;②求
的等距点;②求![]() 的值.
的值.
【答案】(1)![]() 或
或 ![]() ; (2)①证明见解析, ②
; (2)①证明见解析, ②![]() .
.
【解析】
(1)根据三角形的等距点的定义得出OB=OE或OA=OF,利用相似三角形,表达出对应边,列出方程求解即可;
(2)①由△CPD为直角三角形,作出外接圆,通过平行线分线段成比例得出DP∥OB,进而证明△CBO≌△PBO,最后推出OP为点O到AB的距离,从而证明点O是△ABC的等距点;
(2)求![]() 相当于求
相当于求![]() ,由①可得△APO为直角三角,通过勾股定理计算出BC的长度,从而求出
,由①可得△APO为直角三角,通过勾股定理计算出BC的长度,从而求出![]() .
.
解:(1)如图所示,作OF⊥BC于点F,作OE⊥AC于点E,
则△OBF∽△ABC,
∴![]()
∵![]() ,
,![]() ,由勾股定理可得AB=5,
,由勾股定理可得AB=5,
设OB=x,则![]()
∴![]() ,
,![]()
∵点![]() 是
是![]() 的等距点,
的等距点,
若OB=OE,![]()
∴![]()
解得:![]()
若OA=OF,OA=5-x
∴![]() ,解得
,解得![]()
故OB的值为![]() 或
或 ![]()
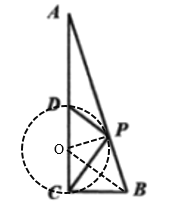
(2) ①证明:∵△CDP是直角三角形,所以取CD中点O,作出△CDP的外接圆,连接OP,OB
设圆O的半径为r,则DC=2r,
∵D是AC中点,
∴OA=3r
∴![]() ,
,
又∵PA=2PB,
∴AB=3PB
∴![]()
∴![]()
∴∠ODP=∠COB,∠OPD=∠POB
又∵∠ODP=∠OPD,
∴∠COB=∠POB,
在△CBO与△PBO中, ,
,
∴△CBO≌△PBO(SAS)
∴∠OCB=∠OPB=90°,
∴OP⊥AB,
即OP为点O到AB的距离,
又∵OP=OC,
∴△CPD的外接圆圆心O是△ABC的等距点
②由①可知,△OPA为直角三角形,且∠PDC=∠BOC,OC=OP=r
∵在Rt△OPA中,OA=3r,
∴![]() ,
,
∴![]()
∴在Rt△ABC中,AC=4r,![]() ,
,
∴![]() ,
,
∴![]()

【题目】某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如图的统计表和扇形图:

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 20 |
B | b | 18 |
C | c | 15 |
(1)①在扇形图中,a= ,C部门所对应的圆心角的度数为 .
②在统计表中,b= ,c= .
(2)求这个公司平均每人所创年利润.
【题目】(10分)学校组织学生参加综合实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售价x(元/双) | 150 | 200 | 250 | 300 |
销售量y(双) | 40 | 30 | 24 | 20 |
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价定为多少元?