题目内容
如图所示,已知平面直角坐标系xOy,抛物线过点A(4,0)、B(1,3)
【小题1】求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
【小题2】记该抛物线的对称轴为直线l,设抛物线上的点P(m,n)在第四象限,点P关于直线l的对称点为E,点E关于y轴的对称点为F,若四边形OAPF的面积为20,求m、n的值.
p;【答案】
【小题1】y=- ,
,
对称轴为:x=2,顶点坐标为:(2,4)
【小题2】m、n的值分别为 5,-5解析:
(1)将点A(4,0)、B(1,3) 的坐标分别代入y=-x2+bx+c,得:
4b+c-16=0 , b+c-1="3" ,解得: b="4" , c=0。
所以抛物线的表达式为: 。
。
y=- ,
,
所以抛物线的对称轴为:x=2,顶点坐标为:(2,4)。
(2)由题可知,E、F点坐标分别为(4-m,n),(m-4,n)。
三角形POF的面积为:1/2×4×|n|= 2|n|,
三角形AOP的面积为:1/2×4×|n|= 2|n|,
四边形OAPF的面积= 三角形POF的面积+三角形AOP的面积=20,
所以 4|n|=20, n=-5。(因为点P(m,n)在第四象限,所以n<0)
又n=- +4m,
+4m,
所以 -4m-5=0,m=5。(因为点P(m,n)在第四象限,所以m>0)
-4m-5=0,m=5。(因为点P(m,n)在第四象限,所以m>0)
故所求m、n的值分别为 5,-5。
【小题1】y=-
 ,
,对称轴为:x=2,顶点坐标为:(2,4)
【小题2】m、n的值分别为 5,-5解析:
(1)将点A(4,0)、B(1,3) 的坐标分别代入y=-x2+bx+c,得:
4b+c-16=0 , b+c-1="3" ,解得: b="4" , c=0。
所以抛物线的表达式为:
 。
。y=-
 ,
,所以抛物线的对称轴为:x=2,顶点坐标为:(2,4)。
(2)由题可知,E、F点坐标分别为(4-m,n),(m-4,n)。
三角形POF的面积为:1/2×4×|n|= 2|n|,
三角形AOP的面积为:1/2×4×|n|= 2|n|,
四边形OAPF的面积= 三角形POF的面积+三角形AOP的面积=20,
所以 4|n|=20, n=-5。(因为点P(m,n)在第四象限,所以n<0)
又n=-
 +4m,
+4m,所以
 -4m-5=0,m=5。(因为点P(m,n)在第四象限,所以m>0)
-4m-5=0,m=5。(因为点P(m,n)在第四象限,所以m>0)故所求m、n的值分别为 5,-5。

练习册系列答案
相关题目
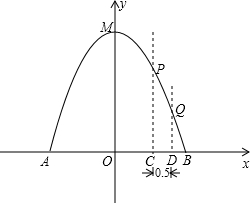 的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.
的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系. B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=
B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=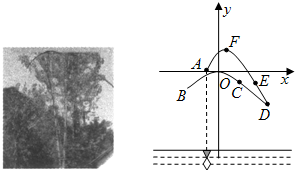 点变为F),假设钓鱼线与人手(点D)的水平距离为
点变为F),假设钓鱼线与人手(点D)的水平距离为 (2012•建阳市模拟)小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊到B′处,紧绷着的吊绳A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=
(2012•建阳市模拟)小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊到B′处,紧绷着的吊绳A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA= 紧绷着的吊缆A′B′=AB.且cosA=
紧绷着的吊缆A′B′=AB.且cosA=