题目内容
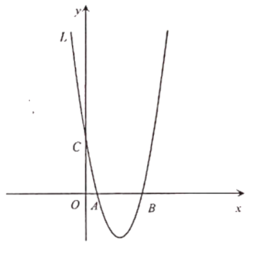
【题目】如图,抛物线![]() 与
与![]() 铀交于
铀交于![]() 两点(点
两点(点![]() 作点
作点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() 且
且![]() ,点
,点![]() 为抛物线
为抛物线![]() 的对称轴右侧图象上的一点.
的对称轴右侧图象上的一点.
(1)a的值为_ ,抛物线的顶点坐标为_ ;
(2)设抛物线![]() 在点
在点![]() 和点
和点![]() 之间部分(含点
之间部分(含点![]() 和点
和点![]() )的最高点与最低点的纵坐标之差为
)的最高点与最低点的纵坐标之差为![]() ,求
,求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
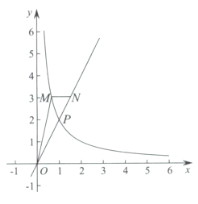
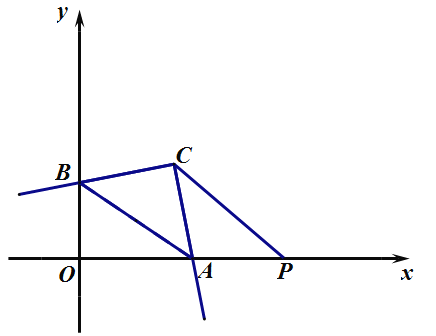
(3)当点![]() 的坐标满足:
的坐标满足:![]() 时,连接
时,连接![]() ,若
,若![]() 为线段
为线段![]() 上一点,且
上一点,且![]() 分四边形
分四边形![]() 的面积为相等两部分,求点
的面积为相等两部分,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时, ![]() 当
当![]() ,
,![]() ;(3)
;(3)![]()
【解析】
(1)根据抛物线![]() 与
与![]() 铀交于
铀交于![]() 两点(点
两点(点![]() 作点
作点![]() 的左侧),可得A点坐标为:(1,0),B点坐标为:(5,0),
的左侧),可得A点坐标为:(1,0),B点坐标为:(5,0),![]() ,则有C点坐标为:(0,5),可得
,则有C点坐标为:(0,5),可得![]() ,抛物线
,抛物线![]() 的函数表达式为:
的函数表达式为:![]() ,得到抛物线的顶点坐标为(3,-4);
,得到抛物线的顶点坐标为(3,-4);
(2)根据抛物线![]() 的函数表达式为:
的函数表达式为:![]() ,得到抛物线
,得到抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,分两种情况:当
,分两种情况:当![]() 时,点
时,点![]() 为最高点,抛物线
为最高点,抛物线![]() 的顶点为最低点,当
的顶点为最低点,当![]() 时,点
时,点![]() 为最高点,抛物线
为最高点,抛物线![]() 的顶点为最低点,分别求出h的函数表达式即可;
的顶点为最低点,分别求出h的函数表达式即可;
(3)根据点![]() (
(![]() )是抛物线
)是抛物线![]() 图象上的点,
图象上的点,![]() ,可得方程
,可得方程![]() ,解得
,解得![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,设直线
,设直线![]() 的函数表达式为
的函数表达式为![]() ,代入P,C两点坐标可求得
,代入P,C两点坐标可求得![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,利用
,利用![]() 分四边形
分四边形![]() 的面积为相等两部分,即:
的面积为相等两部分,即:![]() ,可得
,可得![]() ,解得
,解得![]() ,
,![]() ,可得点
,可得点![]() 的坐标为
的坐标为![]() .
.
解:(1)∵抛物线![]() 与
与![]() 铀交于
铀交于![]() 两点(点
两点(点![]() 作点
作点![]() 的左侧),
的左侧),
∴A点坐标为:(1,0),B点坐标为:(5,0),
∴![]()
∴C点坐标为:(0,5),
即:![]()
∴![]() ,
,
∴抛物线![]() 的函数表达式为:
的函数表达式为:![]() ,
,
∴抛物线的顶点坐标为(3,-4);
(2)由(1)可知:抛物线![]() 的函数表达式为:
的函数表达式为:![]()
![]() 当
当![]() 时,
时,![]() ,
,
![]() .
.
抛物线![]() 的对称轴为直线
的对称轴为直线![]() .
.
当![]() 时,点
时,点![]() 为最高点,抛物线
为最高点,抛物线![]() 的顶点为最低点,
的顶点为最低点,
![]()
当![]() 时,点
时,点![]() 为最高点,抛物线
为最高点,抛物线![]() 的顶点为最低点,
的顶点为最低点,
![]()
(3)∵点![]() (
(![]() )是抛物线
)是抛物线![]() 图象上的点,
图象上的点,
![]()
又![]() ,
,
![]()
![]()
即![]()
![]() (舍),
(舍),
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的函数表达式为
的函数表达式为![]()
![]() ,
,
解得![]()
![]() .
.
设点![]() 的坐标为
的坐标为![]() ,
,
连接![]()

![]()
![]()
![]()
解得![]()
![]()
![]() 点
点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
相关题目