题目内容
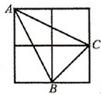
 如图,由四个边长为1的小正方形构成一个大正方形,BC边上的高是
如图,由四个边长为1的小正方形构成一个大正方形,BC边上的高是3
| ||
| 3 |
3
| ||
| 3 |
分析:用正方形的面积减去三角形ACD、ABE、CBF的面积可得出答案.
解答:解:由题意知,小四边形分别为小正方形,所以B、C为EF、FD的中点,
S△ABC=S正方形AEFD-S△AEB-S△BFC-S△CDA
=2×2-
×1×2-
×1×1-
×1×2,
=
.
BC=
=
.
则△ABC中BC边上的高是
×2÷
=
.
故答案为:
.

S△ABC=S正方形AEFD-S△AEB-S△BFC-S△CDA
=2×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
BC=
| 12+12 |
| 2 |
则△ABC中BC边上的高是
| 3 |
| 2 |
| 2 |
3
| ||
| 2 |
故答案为:
3
| ||
| 2 |
点评:本题考查了勾股定理,直角三角形面积的计算,正方形各边相等的性质,本题中,正确的运用面积加减法计算结果是解题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
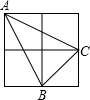 如图,由四个边长为1的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是
如图,由四个边长为1的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是 .
.
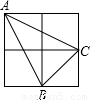
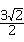 .
.