题目内容
 已知,如图,△ABC中,DE∥BC,AD:DB=3:2,则S△ADE:S四边形BCED=
已知,如图,△ABC中,DE∥BC,AD:DB=3:2,则S△ADE:S四边形BCED=
- A.8:15
- B.9:25
- C.13:17
- D.9:16
D
分析:由DE∥BC,可得△ADE∽△ABC,又由AD:DB=3:2,即可得AD:AB=3:5,然后根据相似三角形面积的比等于相似比的平方,即可求得S△ABC:S△ABC的值,继而求得答案.
解答:∵DE∥BC,
∴△ADE∽△ABC,
∴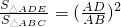 ,
,
∵AD:DB=3:2,
∴AD:AB=3:5,
∴S△ADE:S△ABC=9:25,
∴S△ADE:S四边形BCED=9:16.
故选D.
点评:此题考查了相似三角形的判定与性质.此题比较简单,注意掌握相似三角形的面积比等于相似比的平方定理的应用是解此题的关键.
分析:由DE∥BC,可得△ADE∽△ABC,又由AD:DB=3:2,即可得AD:AB=3:5,然后根据相似三角形面积的比等于相似比的平方,即可求得S△ABC:S△ABC的值,继而求得答案.
解答:∵DE∥BC,
∴△ADE∽△ABC,
∴
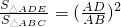 ,
,∵AD:DB=3:2,
∴AD:AB=3:5,
∴S△ADE:S△ABC=9:25,
∴S△ADE:S四边形BCED=9:16.
故选D.
点评:此题考查了相似三角形的判定与性质.此题比较简单,注意掌握相似三角形的面积比等于相似比的平方定理的应用是解此题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N. 已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.
已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长. 已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.
已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE. 已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A. 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.