题目内容
已知AB 是⊙O 的直径,点 P 在线段 AB 的延长线上,BP=OB=2,点 Q 在⊙O 上,连接 PQ.
(Ⅰ)如图①,线段 PQ 所在的直线与⊙O 相切,求线段 PQ 的长;
(Ⅱ)如图②,线段 PQ 与⊙O 还有一个公共点 C,且 PC=CQ,求线段 PQ 的长.
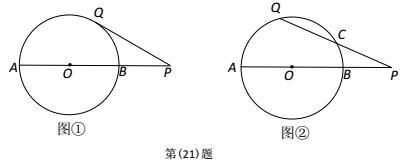
(Ⅰ)解:连接 QO.
∵ 线段 PQ 所在的直线与⊙O 相切,点 Q 在⊙O 上, ∴ OQ⊥QP,即∠OQP=90°.
又∵OQ= OB ,BP=OB =2,∴OQ=2,OP=4. ∴ PQ= 即线段 PQ 的长为
即线段 PQ 的长为 .
.
(Ⅱ)解:过点 O 作 OE⊥QC,垂足为 E,连接 QO.
∵ OE⊥QC,垂足为 E, ∴ QE=EC. 设 QE=x ,则 EC=x ,QC=2x.
∵PC=CQ,∴PC=2x,PE=3x,PQ=4x.
由(Ⅰ)知 OQ=2,OP=4. ∴ 在 Rt△QOE 中, OE 2= OQ 2 -QE 2 = 22-x 2 ,
在 Rt△POE 中, OE 2 = OP 2- PE 2 = 42- 9x 2 , ∴ 22- x 2 = 42-9x 2 ,
解这个方程,得  (不合题意,舍).
(不合题意,舍).
∴ PQ=4x= 4× =
= .即线段 PQ 的长为
.即线段 PQ 的长为 .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
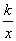 (x>0,k≠0)的图象经过线段BC的中点D.
(x>0,k≠0)的图象经过线段BC的中点D.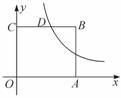

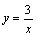 ,下列结论中,正确的是( )
,下列结论中,正确的是( )

 B.
B.
 C.
C.
 D.
D.


 D.﹣
D.﹣ ____ _____.
____ _____.