题目内容
19.已知关于x、y的方程组$\left\{\begin{array}{l}{x+2y=k}\\{2x+3y=3k-1}\end{array}\right.$的解x、y的值的和等于6,求k的值.分析 方程组两方程相减表示出x+y,根据x、y的值的和为6求出k的值即可.
解答 解:$\left\{\begin{array}{l}{x+2y=k①}\\{2x+3y=3k-1②}\end{array}\right.$,
②-①得:x+y=2k-1,
由题意得:x+y=6,
∴2k-1=6,
解得:k=$\frac{7}{2}$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列方程组中,哪项的解是$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$( )
| A. | $\left\{\begin{array}{l}{x+y=1}\\{x-y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x-2y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x=y}\\{y+x=-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{6}=1}\\{x+y=3}\end{array}\right.$ |
7. 如图,实数-3,x,3,y在数轴上的对应点分别为M、N、P、Q,这四个数中绝对值最大的数对应的点是( )
如图,实数-3,x,3,y在数轴上的对应点分别为M、N、P、Q,这四个数中绝对值最大的数对应的点是( )
 如图,实数-3,x,3,y在数轴上的对应点分别为M、N、P、Q,这四个数中绝对值最大的数对应的点是( )
如图,实数-3,x,3,y在数轴上的对应点分别为M、N、P、Q,这四个数中绝对值最大的数对应的点是( )| A. | 点M | B. | 点N | C. | 点P | D. | 点Q |
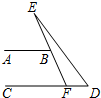 如图,AB∥CD,∠ABE=60°,则∠EFD的度数为120°.
如图,AB∥CD,∠ABE=60°,则∠EFD的度数为120°. 如图,在斜坡CM上有一棵大树AB(与水平线垂直),坡面CM与水平线CN的夹角为37°,在斜坡底端C点处测得大树顶端A的仰角为53°,已知BC间的距离为10米,求大树的高(最终结果保留整数).(参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin53°≈$\frac{4}{5}$,tan53°≈$\frac{4}{3}$).
如图,在斜坡CM上有一棵大树AB(与水平线垂直),坡面CM与水平线CN的夹角为37°,在斜坡底端C点处测得大树顶端A的仰角为53°,已知BC间的距离为10米,求大树的高(最终结果保留整数).(参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin53°≈$\frac{4}{5}$,tan53°≈$\frac{4}{3}$).