题目内容
【题目】如图，二次函数图象过A，B，C三点，点A的坐标为（﹣1，0），点B的坐标为（4，0），点C在y轴正半轴上，且AB＝OC．
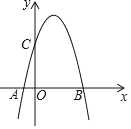
（1）求点C的坐标；
（2）求二次函数的解析式．
【答案】（1）C点的坐标为（0，5）；（2）y＝﹣
x2+
x+5．
【解析】
（1）先求出AB，再求出OC，即可得出C的坐标；
（2）把A、B、C的坐标代入函数解析式，即可求出a、b、c的值，即可得出答案．
解：（1）∵点A的坐标为（﹣1，0），点B的坐标为（4，0），
∴AB＝1+4＝5，
∵AB＝OC，
∴OC＝5，
∴C点的坐标为（0，5）；
（2）设过A、B、C点的二次函数的解析式为y＝ax2+bx+c，
把A、B、C的坐标代入得：
，
解得：a＝﹣，b＝，c＝5，
所以二次函数的解析式为y＝﹣x2+x+5．
练习册系列答案
相关题目
