题目内容
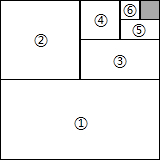 如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.
如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.(1)阴影部分的面积是
| 1 |
| 64 |
| 1 |
| 64 |
(2)如果继续分割下去,部分
 的面积为
的面积为| 1 |
| 2n |
| 1 |
| 2n |
(3)受此启发,请你求出
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 26 |
| 63 |
| 64 |
| 63 |
| 64 |
分析:观察图形发现部分①的面积为:
,部分②的面积为:
=
,…,部分 的面积
的面积
,据此规律解答即可.
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 4 |
 的面积
的面积| 1 |
| 2n |
解答:解:∵观察图形发现部分①的面积为:
,部分②的面积为:
=
,…,部分 的面积
的面积
,
∴(1)阴影部分的面积是
=
;
(2)如果继续分割下去,部分 的面积为
的面积为
;
(3)
+
+
+…+
=1-
=
,
故答案为:
,
;
.
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 4 |
 的面积
的面积| 1 |
| 2n |
∴(1)阴影部分的面积是
| 1 |
| 26 |
| 1 |
| 64 |
(2)如果继续分割下去,部分
 的面积为
的面积为| 1 |
| 2n |
(3)
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 26 |
| 1 |
| 26 |
| 63 |
| 64 |
故答案为:
| 1 |
| 64 |
| 1 |
| 2n |
| 63 |
| 64 |
点评:本题考查了图形的变化类问题,解题的关键是仔细观察图形并发现图形变化的规律.

练习册系列答案
相关题目
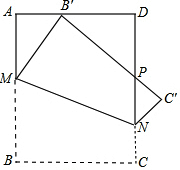
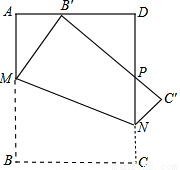
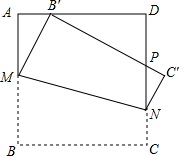 (2012•河东区二模)如图,将一个边长为1的正方形纸片ABCD折叠,使点B落在边AD上(不与A、D重合),MN为折痕,折叠后B′C′与DN交于P,则四边形MNC′B′面积最小值为
(2012•河东区二模)如图,将一个边长为1的正方形纸片ABCD折叠,使点B落在边AD上(不与A、D重合),MN为折痕,折叠后B′C′与DN交于P,则四边形MNC′B′面积最小值为