题目内容
在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.
⑴求证:Rt△ABE≌Rt△CBF;
⑵若∠CAE=30º,求∠ACF度数.
⑴见解析⑵60º解析:
⑴∵AB=CB,∠ABC=90º，AE=CF
∴Rt△ABE≌Rt△CBF
⑵∵Rt△ABE≌Rt△CBF
∴∠BAE=∠BCF
∵AB=CB,∠ABC=90º,
∴∠BAC=∠BCA=45º
∵∠CAE=30º
∴∠BAE=15º
∴∠BCF=15º
∴∠ACF=∠BCF+∠BCA=15º+45º=60º
⑴根据斜边和一条直角边对应相等的两个直角三角形全等判定
⑵利用全等三角形的性质求解
⑴∵AB=CB,∠ABC=90º，AE=CF
∴Rt△ABE≌Rt△CBF
⑵∵Rt△ABE≌Rt△CBF
∴∠BAE=∠BCF
∵AB=CB,∠ABC=90º,
∴∠BAC=∠BCA=45º
∵∠CAE=30º
∴∠BAE=15º
∴∠BCF=15º
∴∠ACF=∠BCF+∠BCA=15º+45º=60º
⑴根据斜边和一条直角边对应相等的两个直角三角形全等判定
⑵利用全等三角形的性质求解
练习册系列答案
阅读快车系列答案
相关题目
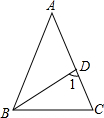如图，在△ABC中AB=AC，∠A=36°，BD平分∠ABC，则∠1=
如图，在△ABC中AB=AC=6cm，BC=8cm．点E是线段BC边上的一动点（不含B、C两端点），连结AE，作∠AED=∠B，交线段AB于点D．
如图：在△ABC中AB=AC，在△BCE中BA平分∠CBE，且BC=2BE．求证：BE⊥AE．
已知，如图，在△ABC中AB=AC，以AB为直径的圆交BC于点D，交AC于点E，