题目内容
 已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为( )
已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为( )| A、9 | ||
| B、3 | ||
C、
| ||
D、
|
分析:①在Rt△ABC中,由勾股定理可得:AC2+BC2=AB2,三角形的面积=
×底×高;
②分别设以Rt△ABC的三边为斜边分别向外作等腰直角三角形的底边上的高分别为h1,h2,h3,由等腰直角三角形“三线合一”的性质和直角三角形斜边上的中线等于斜边的一半,可得出斜边上的高=
×斜边的长;
③阴影部分的面积=三个等腰三角形的面积之和.
| 1 |
| 2 |
②分别设以Rt△ABC的三边为斜边分别向外作等腰直角三角形的底边上的高分别为h1,h2,h3,由等腰直角三角形“三线合一”的性质和直角三角形斜边上的中线等于斜边的一半,可得出斜边上的高=
| 1 |
| 2 |
③阴影部分的面积=三个等腰三角形的面积之和.
解答:解:设以Rt△ABC的三边为斜边分别向外作等腰直角三角形的底边上的高分别为h1,h2,h3,
则h1=
AC,h2=
BC,h3=
AB,
即:阴影部分的面积为:
×
×AC×AC+
×
×BC×BC+
×
×AB×AB=
(AC2+AB2+BC2),
在Rt△ABC中,由勾股定理可得:AC2+BC2=AB2,AB=3,
所以阴影部分的面积为:
×2AB2=
×32=
,
故选D.
则h1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即:阴影部分的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
在Rt△ABC中,由勾股定理可得:AC2+BC2=AB2,AB=3,
所以阴影部分的面积为:
| 1 |
| 4 |
| 1 |
| 2 |
| 9 |
| 2 |
故选D.
点评:本题主要考查运用勾股定理求出等腰直角三角形三条斜边之间的关系,并利用此关系求出三个三角形面积之间的关系,进而求出总面积,阴影部分的面积=各个阴影部分的面积之和.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
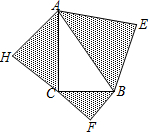 已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形,若斜边AB=5,则图中阴影部分的面积为
已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形,若斜边AB=5,则图中阴影部分的面积为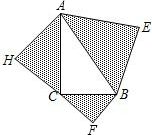 已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=6,则图中阴影部分的面积为
已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=6,则图中阴影部分的面积为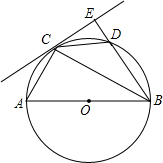 已知:如图,以Rt△ABC的斜边AB为直径作⊙O,D是⊙O上的点,且有AC=CD.过点C作⊙O的切线,与BD的延长线交于点E,连接CD.
已知:如图,以Rt△ABC的斜边AB为直径作⊙O,D是⊙O上的点,且有AC=CD.过点C作⊙O的切线,与BD的延长线交于点E,连接CD. 已知,如图,以Rt△ABC的斜边AB为直径作⊙0,D是BC上的点,且有弧AC=弧CD,连CD、BD,在BD延长线上取一点E,使∠DCE=∠CBD.
已知,如图,以Rt△ABC的斜边AB为直径作⊙0,D是BC上的点,且有弧AC=弧CD,连CD、BD,在BD延长线上取一点E,使∠DCE=∠CBD. 已知:如图,以Rt△ABC的直角边AC为直径作⊙O,交AB于D点,OE∥AB交BC于E点,求证:DE为⊙O的切线.
已知:如图,以Rt△ABC的直角边AC为直径作⊙O,交AB于D点,OE∥AB交BC于E点,求证:DE为⊙O的切线.