Question

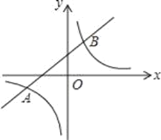
【题目】一块直角三角板ABC按如图放置，顶点A的坐标为（0，1），直角顶点C的坐标为（﹣3，0），∠B=30°，则点B的坐标为 ．

Answer 1

【答案】（﹣3﹣，3）．

【解析】

过点B作BD⊥OD于点D，根据△ABC为直角三角形可证明△BCD∽△COA，设点B坐标为（x，y），根据相似三角形的性质即可求解．

过点B作BD⊥OD于点D，

∵△ABC为直角三角形，

∴∠BCD+∠ACO=90°，

∴∠ACO＋∠CAO=90°,

∴∠BCD=∠CAO（同角的余角相等），

∵∠AOC=∠BDC=90°，

∴△BCD∽△COA，

∴，

设点B坐标为（x，y），则，

∴y=﹣3x﹣9，

∴由勾股定理得：BC==，

而AC==，

∵∠B=30°，

∴，解得：x=﹣3±，

∵x<0,∴x=﹣3-,则y=3，

即点B的坐标为（﹣3﹣，3）．