题目内容
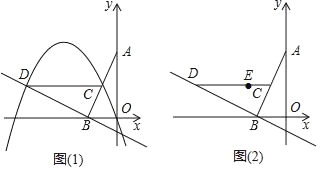
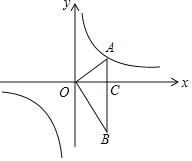
【题目】如图，在平面直角坐标系中，点
在反比例函数
的图象上，
，
轴于点C．
求反比例函数的表达式；
求
的面积；
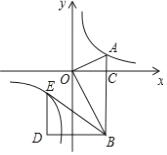
若将
绕点B按逆时针方向旋转
得到
点O、A的对应点分别为
、
，点
是否在反比例函数的图象上？若在请直接写出该点坐标，若不在请说明理由．
【答案】（1）
；（2）
的面积为
；（3）点E在该反比例函数的图象上
理由见解析
【解析】
将点
代入
，利用待定系数法即可求出反比例函数的表达式
先由射影定理求出
，那么
，计算出
先解
，得出
，再根据旋转的性质求出E点坐标为
，即可求解．
点，在反比例函数的图象上，
，
反比例函数的表达式为
；
点，
轴于点，
，
，
由射影定理得
，可得，点，
，
故的面积为；
点E在该反比例函数的图象上
理由如下：
，
，
，
，
，
，
将
绕点B按逆时针方向旋转
得到
，如图，
≌，
，
，
，
，
，
而
，
，
点E的坐标为，
，
点E在该反比例函数的图象上.
练习册系列答案
相关题目
