题目内容
已知实数a，b满足
，且ax+b=0，求
的值．
解：由非负数的性质知a-2=0且b+4=0，
解得a=2，b=-4．
∴2x-4=0，
解得x=2．
∴
=
．
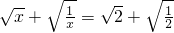分析：两项非负数之和等于0，可分别求出a和b的值，代入ax+b=0，可求出x．然后代入题中式子即可．
点评：此题考查了非负数的性质，求出a和b的值是关键．
解得a=2，b=-4．
∴2x-4=0，
解得x=2．
∴
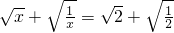=．分析：两项非负数之和等于0，可分别求出a和b的值，代入ax+b=0，可求出x．然后代入题中式子即可．
点评：此题考查了非负数的性质，求出a和b的值是关键．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
已知实数a、b满足a＜b，则下列式子中正确的是（ ）
A、
| ||||
| B、b-a＞0 | ||||
| C、a2＜b2 | ||||
| D、a4＜b4 |