题目内容
【题目】定义感知：我们把顶点关于
轴对称，且交于轴上同一点的两条抛物线叫做“孪生抛物线”，该点叫“孪生抛物线”的“共点”．如图所示的抛物线
与
是一对“孪生抛物线”，其“共点”为点
．
初步运用：
判断下列论断是否正确？正确的在题后横线上打“√”，错误的则打“
”：
①“孪生抛物线”的“共点”不能分布在
轴上．________
②“孪生抛物线”
与
的“共点”坐标为
．________
填空：抛物线
的“孪生抛物线”的解析式为________．
延伸拓展：在平面直角坐标系中，记“孪生抛物线”的两顶点分别为
，
，且
，其“共点”与，，
三点恰好构成一个面积为
的菱形，试求该“孪生抛物线”的解析式．
【答案】
√
【解析】
初步运用：（1）由“孪生抛物线”的意义判断即可，它们的共点在y轴，求出其坐标；
（2）由“孪生抛物线”的顶点关于y轴对称，所以把解析式化成顶点式，求出其“孪生抛物线”；
延伸拓展：由于其“共点”A与M，M′，O三点恰好构成一个面积为12的菱形，且MM′=4，①开口向上时，求出M（-2，3），M′（2，3），A（0，6），设出“孪生抛物线”把共点A（0，6）代入即可，②开口向下时，求出M（-2，-3），M′（2，-3），A（0，-6），设出“孪生抛物线”把共点A（0，-6）代入即可．
初步运用：
（1）①∵把顶点关于y轴对称，且交于y轴上同一点的两条抛物线叫做“孪生抛物线”，该点叫“孪生抛物线”的“共点”．
∴“孪生抛物线”的“共点”能分布在x轴上，
②∵交于y轴上同一点的两条抛物线叫做“孪生抛物线”，该点叫“孪生抛物线”的“共点”，
∴“孪生抛物线”的“共点”在y轴上，
②“孪生抛物线”y=（x-2）2-9与y=（x+2）2-9
∴令x=0，y=5，
∴共点（0，5）
故答案为×，√
（2）∵抛物线y=-2x2-4x+5=-2（x2+2x）+5=-2（x+1）2+7，
∴它的“孪生抛物线”为y=-2（x-1）2+7=-2（x2-2x+1）+7=-2x2+4x+5，
故答案为y=-2x2+4x+5；
延伸拓展：由题意得，“孪生抛物线”有下面两种情况：
①当“孪生抛物线”的开口向上时，如图1所示，
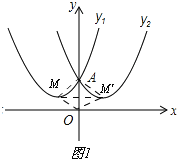
∵由于其“共点”A与M，M′，O三点恰好构成一个面积为12的菱形，且MM′=4，
∴
MM′×OA=12，
∴OA=6，
∴M（-2，3），M′（2，3），A（0，6），
由此可设“孪生抛物线”的解析式为：y=a（x+2）2+3与y=a（x-2）2+3，
∵点A（0，6）在“孪生抛物线”的图象上，
∴6=a×22+3，
∴a=
，
∴“孪生抛物线”的解析式为：y=（x+2）2+3与y=（x-2）2+3；
②当“孪生抛物线”的开口向下时，如图2所示，
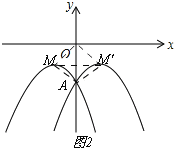
∵由于其“共点”A与M，M′，O三点恰好构成一个面积为12的菱形，且MM′=4，
∴MM′×OA=12，
∴OA=6，
∴M（-2，-3），M′（2，-3），A（0，-6），
由此可设“孪生抛物线”的解析式为：y=a（x+2）2-3与y=a（x-2）2-3，
∵点A（0，-6）在“孪生抛物线”的图象上，
∴-6=a×22+3，
∴a=-，
∴“孪生抛物线”的解析式为：y=-（x+2）2+3与y=-（x-2）2+3；
