题目内容
已知△ABC中,满足| 1 | ||
tan
|
| 1 | ||
tan
|
| 4 | ||
tan
|
分析:作△ABC的内切圆,设O为圆心,r为半径,圆O与三边AB、BC、AC的切点依次为D、E、F,连接OA、OB、OC、OD、OE、OF,则OA、OB、OC平分△ABC的三个内角.根据正切函数的定义及已知条件,可得BD=1,然后根据切线长定理即可求出a+c的值.
解答: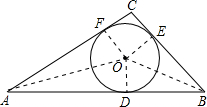 解:如图,作△ABC的内切圆,设O为圆心,r为半径,圆O与三边AB、BC、AC的切点依次为D、E、F,连接OA、OB、OC、OD、OE、OF.
解:如图,作△ABC的内切圆,设O为圆心,r为半径,圆O与三边AB、BC、AC的切点依次为D、E、F,连接OA、OB、OC、OD、OE、OF.
则tan
=
,tan
=
,tan
=
.
∵
+
=
,
∴
+
=
,
∴AF+CF=4BD,即AC=4BD,
又∵b=AC=4,
∴BD=1,
∴BE=BD=1,
∴a+c=(BE+CE)+(BD+AD)=(CE+AD)+(BE+BD)=b+2BD=6.
故答案为6.
 解:如图,作△ABC的内切圆,设O为圆心,r为半径,圆O与三边AB、BC、AC的切点依次为D、E、F,连接OA、OB、OC、OD、OE、OF.
解:如图,作△ABC的内切圆,设O为圆心,r为半径,圆O与三边AB、BC、AC的切点依次为D、E、F,连接OA、OB、OC、OD、OE、OF.则tan
| B |
| 2 |
| r |
| BD |
| A |
| 2 |
| r |
| AF |
| C |
| 2 |
| r |
| CF |
∵
| 1 | ||
tan
|
| 1 | ||
tan
|
| 4 | ||
tan
|
∴
| AF |
| r |
| CF |
| r |
| 4BD |
| r |
∴AF+CF=4BD,即AC=4BD,
又∵b=AC=4,
∴BD=1,
∴BE=BD=1,
∴a+c=(BE+CE)+(BD+AD)=(CE+AD)+(BE+BD)=b+2BD=6.
故答案为6.
点评:本题考查了三角形的内切圆的性质,正切函数的定义,切线长定理,综合性较强,有一定难度.关键是作辅助线.

练习册系列答案
相关题目
 19、如图,已知△ABC中,DF∥AC,EF∥AB,AF平分∠BAC.
19、如图,已知△ABC中,DF∥AC,EF∥AB,AF平分∠BAC.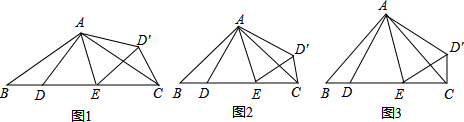
 ,b=4,则a+c=________.
,b=4,则a+c=________. ,b=4,则a+c= .
,b=4,则a+c= .